Non-destructive allometric models for leaf area prediction of Jatropha curcas L.

Krishan Kumar Verma; Chhedi Lal Verma; Munna Singh; Krishan Kumar Verma; Chhedi Lal Verma; Munna Singh

ISSN: 2455-815X

International Journal of Agricultural Science and Food Technology

Research Article Open Access Peer-Reviewed

Non-destructive allometric models for leaf area prediction of Jatropha curcas L.

Krishan Kumar Verma*, Chhedi Lal Verma and Munna Singh

Author and article information

Visiting Scientist, Sugarcane Research Center, Chinese Academy of Agricultural Sciences (CAAS) and Guangxi Academy of Agricultural Sciences (GXAAS), # 174, East Daxue Road, Nanning – 530 007, Guangxi, China

*Corresponding author: Dr. Krishan Kumar Verma, Visiting Scientist, Sugarcane Research Center, Chinese Academy of Agricultural Sciences (CAAS) and Guangxi Academy of Agricultural Sciences (GXAAS), # 174, East Daxue Road, Nanning-530 007, Guangxi, China, Tel: +86 17677637672; E-mail: drvermakishan@gmail.com

DOI: 10.17352/2455-815X.000129

Received: 30 August, 2021 | Accepted: 09 November, 2021 | Published: 10 November, 2021

Keywords: Allometric model; Leaf length; Leaf width; Leaf margin; Leaf area; Jatropha curcas

Cite this as

: Krishan Kumar V, Verma CL, Singh M (2021) Non-destructive allometric models for leaf area prediction of Jatropha curcas L. J Agric Sc Food Technol 7(3): 341-346. DOI: 10.17352/2455-815X.000129

Copyright

© 2021 Krishan Kumar V, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Abstract

Jatropha curcas received a lot of attention as a biodiesel feedstock in several countries around the world. The leaf area (LA) estimation is important for biological research due to its close relationship to soil fertility, plant physiological parameters, and photosynthetic efficiency. Allometric models for reliable and accurate models for estimating the leaf area of Jatropha curcas plants based on non-destructive measurements of leaf length (L), width (W), and/ or leaf margins length (P) were developed. Jatropha plant leaves were randomly selected for model construction to estimate the leaf area using L, W, and P leaf values. Simple and accurate equations were obtained, based on leaf width (A_L = W^1.795), R² = 0.987, rib length (A_L = L₃^2.081), R² = 0.989, width and rib length (A_L = LW^0.320), R2 = 0.997, rib length and leaf periphery segment (A_L = LP₁P₁₂^0.274), R² = 0.995, and half rib and width length (A_L = LW/0.5^0.467), R² = 0.994. The equations were accurate for estimating leaf area of small, medium, and large size of Jatropha leaves.

Main article text

Introduction

Global fuel reserves are decreasing, and fuel prices increase continuously, putting tremendous pressure on developing economies. Fossil fuel deposits are rapidly diminishing, and their consumption raises carbon dioxide discharge levels. Alternative fuels, such as bioethanol and biodiesel, show great promise for mitigating the problems caused by fossil fuel consumption. The various scientific communities are searching for alternative sources of fossil fuel [1-3]. Jatropha curcas L. is a multipurpose plant with a drought-resistant oil species widely distributed in tropical and subtropical areas. It easily grows in Central and South America, Africa, India, and Southeast Asia. It has gained importance for the production of biodiesel [3-5]. Because their seeds contain between 25-32% oil [6,7]. Different parts of Jatropha curcas have also been used for various purposes, such as animal feed, pharmaceutical, economic, and ecosystem restoration of disturbed areas [8-10]. Most importantly, Jatropha curcas seeds contain viscous oil used for soap making in the cosmetics industry and as a diesel/kerosene substitute or extender [9,10].

Jatropha curcas is receiving a lot of attention as biodiesel feedstock. Interests of project managers, investors, and farmers are triggered by the plant’s alleged potential to simultaneously reclaim wastelands, enhance socio-economic development and conserve and/or restore soil fertility in degraded areas [11-14]. These promising characteristics of the Jatropha farming system have resulted in numerous Jatropha plantation initiatives in the semi-arid areas [15]. Current scientific knowledge on the utility of Jatropha biomass is elaborated by the researchers [2,14,16-20]. And seed yield [13,14,20]. The government departments and NGOs are recommending jatropha plantation as a possible source of bio-diesel on waste and unattended lands in the world. Wastelands have poor fertility, flooding, or salt accumulation in the root zone [1,3]. Jatropha grows well on poor stony soils. Therefore, it is recommended for cultivation on degraded soils [2,21]. In tropical and subtropical regions globally [7,22].

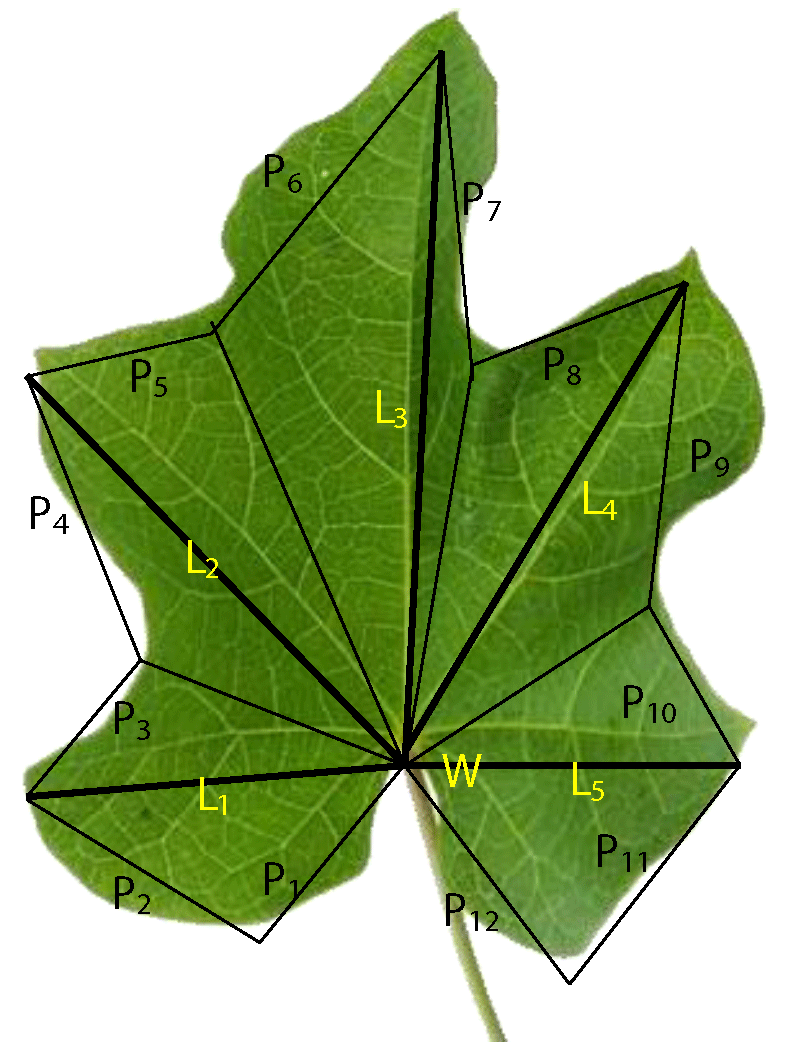
Leaf area (LA) is a key variable for most agronomic and physiological studies involving plant growth, light interception, photosynthetic efficiency, evapotranspiration, and responses to fertilizers and irrigation [23,24]. Photosynthesis and transpiration rate affect plant growth, development, and yield, closely related to leaf area expansion [3,10,13,25]. There are numerous ways for measuring leaf area; however, the length of ribs (L₁, L₂, L₃, L₄, and L₅), width (W), and segment of leaf periphery length (P₁, P₂, P₃ - P₁₁ and P₁₂) as shown in figure 1 are usually easy to measure. In contrast, other features are not easily determined directly (leaf area, mass, volume). Calculation of leaf area through an equation is the most suitable fast, simple, non-destructive method and does not depend on any complex device. Estimating leaf area through equations works better when the measures to be taken can be easily and correctly identified, and the equation is based on only one or a few measures. The equation should estimate an area close to the accurate leaf area and be stable when measuring leaves of different shapes and sizes. A modeling approach involving linear relationships between leaf area and one or more leaf dimensions is a cheap, rapid, reliable, and non-destructive alternative for an accurate leaf area measurement [26]. Non-destructive methods do not require leaves to be detached and reduce the variability associated with destructive sampling procedures, which is important because measurements must be repeated during the plant’s growth period [27-28].

The development of statistical regression models from linear leaf measurements to predict individual leaf area is very useful in studying plant growth and development [7]. Therefore, models for the non-destructive prediction of the leaf area, i.e. allometry, are helpful tools for researchers. In the present study, we evaluate the currently used models [7,13,24]. And proposed simple, reliable, and accurate models using non-destructive measurements of L, W, and/or P for estimating the leaf area of Jatropha leaves.

Material and method

Leaves were collected from a three-year-old Jatropha plant at the Department of Botany, University of Lucknow, Lucknow, Uttar Pradesh, India, to estimate leaf area. More than a hundred plant leaves (n = 100) of the big, medium, and small sizes were used. Jatropha leaves were calculated by available allometric methods and measured by leaf area meter (CI-203, Area Meter, CID. Inc., USA).

Jatropha leaf is irregular but zygomorphic. Measurement of leaf area using a leaf area meter is possible, but it is a destructive procedure. There is a necessity to develop a simple mathematical relationship for measuring leaf area using simple linear measurements. In the present study, linear and nonlinear power form relationships were developed to calculate leaf area with possible linear measurements of leaf dimension.

The dimensions of a Jatropha leaf are twelve (12) linear peripheral segments (P), rib length (L), and cross width (W). Eighteen (18) linear measurements describe jatropha leaf: twelve (12) linear periphery (P), six (6) rib lengths (L), and one cross width (W= L₁+L₅). All of the measurements are interrelated and interdependent. There are correlations between these metrics as well. As a result, the leaf area of Jatropha is linked to these linear measurements, with mini-curves in the leaf toward the petiole side taken into consideration by a constant. A tiny triangle is a component of any two-dimensional form. As a result, Jatropha can be conceived as having a shape similar to a triangle, as depicted in figure 1. The Jatropha leaf is made up of ten triangles that can be shown as a single leaf.

Jatropha plant leaves were selected from different plants and measured to develop the best fitting model to predict the leaf area. The lengths of the leaf ribs (from lamina tip to the point of the petiole), widths (the widest linear length perpendicular to the L₃), and leaf periphery segments were measured. Jatropha leaf has five ribs (L). L₃ (midrib) is the most extended rib of the leaf. The linear length of these ribs determines the shape and size of the Jatropha leaves. All the ribs join at the petiole. The tip of every rib looks like a crest. Between two crests of rib exists a valley. The line joining petiole and lowest point of the valley are termed a dividing line. Thus there are four divide lines in a typical Jatropha leaf.

Statistical analysis

The experimental data were organized, processed, and analyzed using Microsoft Excel and presented as ± SD.

Results

Interdependence of linear measurements

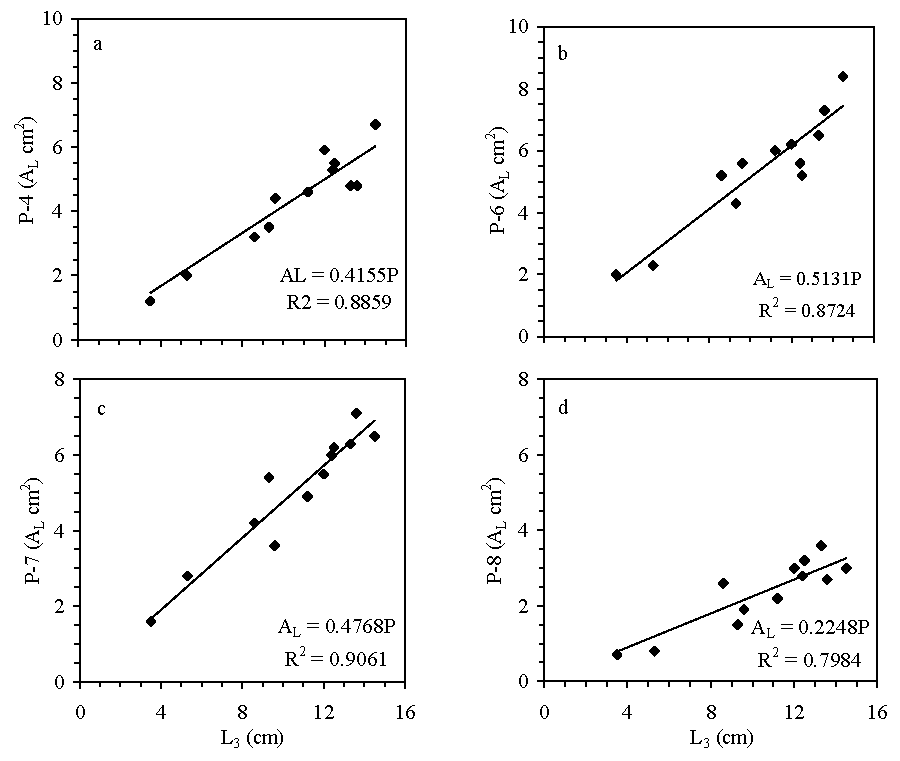
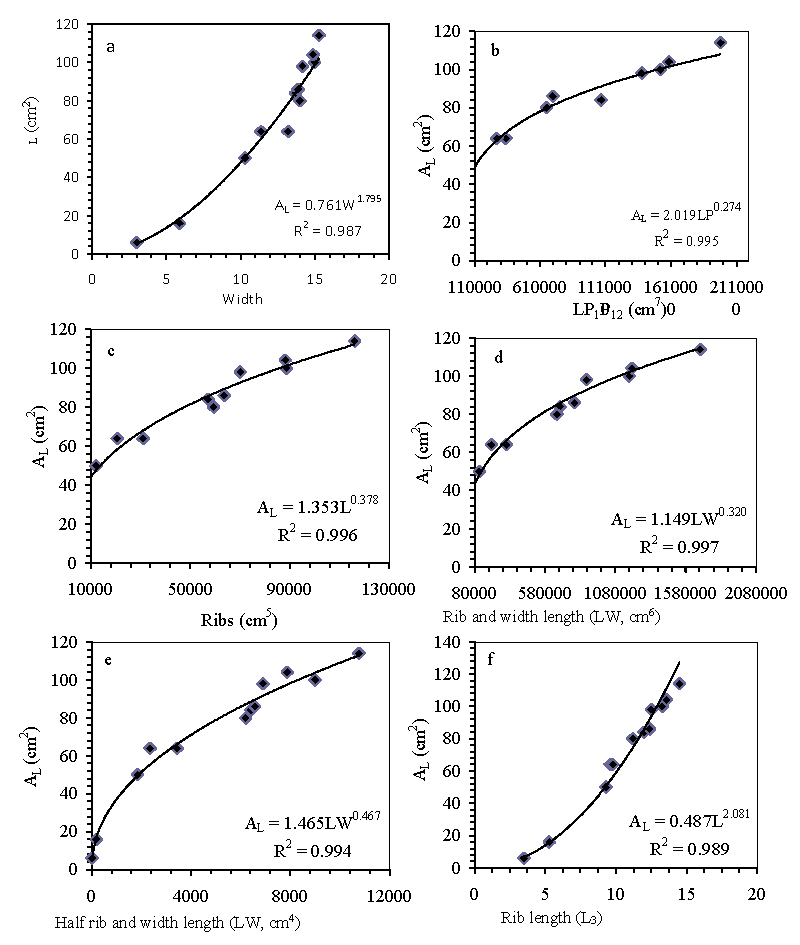
Jatropha leaf has twelve (12) well-defined points. Lines joining these points are defined in Figure 1. There are twelve peripheral segments. The whole Jatropha leaf can be divided into ten triangles. The rib lengths (L) and peripheral segments (P) are interdependent and can be co-related with the midrib length (L₃). Each leaf perimeter segment can be denoted as P₁ - P₁₂ in the clockwise direction. Figure 2 shows that the interdependence of perimeter segmental length with the midrib length. The coefficient of determination (R²) ranged for perimeter segmental lengths with midrib length from 0.517 - 0.906. The perimeter segment is not very strong and easily affects climatic variables, insects, disease and pests, moisture, and nutrient availability. The coefficient of determination of periphery of Jatropha leaf and midrib length is very high (R²= 0.906). Therefore, the periphery of segment lengths, width, and rib lengths can be used for characterizing the Jatropha leaf area. For better understanding, L₃ length and W seem to be more appropriate for describing leaf area. The combination of length and width together should give a more accurate estimate. Regression analysis was done between leaf area (A_L), and midrib length (L), leaf area and leaf width (W), leaf area, and product of midrib length and width (WL) are shown in Figure 3. Regression equations are shown in Table 1. The lowest coefficient of determination was 0.969 for Model No. 17, which shows the variation of leaf area with half rib length and maximum coefficient of determination, i.e., 0.997 was observed for Model No. 13, which is based on the relationship between the product of rib lengths and leaf width.

Table 1. Statistical models, regression coefficients, coefficient of determination, and leaf area (A_L) equations as a function of linear dimensions of (L, W, and P) Jatrophaleaves.
Model no.	Model	Coefficients	R2	Estimator of leaf area (A_L)
1.	A_L = aL32 + bL3	a = 0.442 b = 1.745	0.985	$0 {.442 L}_{3}^{2} + 1.745 L_{3}$
2.	A_L = aL32	a = 0.582	0.978	$0 {.582 L}_{3}^{2}$
3.	A_L = aL3b	a = 0.487	0.989	$0 {.487 L}_{3}^{2.081}$
4.	A_L = aWb	a = 0.761	0.987	$0 .761 W_{}^{1.795}$
5.	A_L = aW2	a = 0.452	0.973	$0 .452 W_{}^{2}$
6.	A_L = aLW	a = 0.516	0.992	$0 .516 L W$
7.	A_L = aLPb	a = 2.019	0.990	$2 .019 (L_{1}^{} L_{2}^{} L_{3}^{} L_{4}^{} L_{5}^{} P_{1}^{} P_{2}^{})^{0 .274}$
8.	A_L = aLPb	a = 1.738	0.995	$1 .738 (L_{1}^{} L_{2}^{} L_{3}^{} L_{4}^{} L_{5}^{} P_{1}^{} P_{2}^{})^{1/7}$
9.	A_L = aLb	a = 1.353	0.996	$1 .353 (L_{1}^{} L_{2}^{} L_{3}^{} L_{4}^{} L_{5}^{})^{0 .378}$
10.	A_L = aLb	a = 1.068	0.986	$1 .068 (L_{1}^{} L_{2}^{} L_{3}^{} L_{4}^{} L_{5}^{})^{\frac{2}{5}}$
11.	A_L = aLWb	a = 1.698	0.996	$1 .698 (L_{1}^{} L_{2}^{} L_{3}^{} L_{4}^{} L_{5}^{} W)^{0.242}$
12.	A_L = aLWb	a = 1.518	0.993	$1 .518 (L_{1}^{} L_{2}^{} L_{3}^{} L_{4}^{} L_{5}^{} W)^{\frac{2}{8}}$
13.	A_L = aLWb	a = 1.149	0.997	$1 .149 (L_{1}^{} L_{2}^{} L_{3}^{} L_{4}^{} L_{5}^{} W)^{0.320}$
14.	A_L = aLW2/6 + b	a = 0.941 b = 2.361	0.990	$1 .149 (L_{1}^{} L_{2}^{} L_{3}^{} L_{4}^{} L_{5}^{} W)^{\frac{2}{6}} + 2.361$
15.	A_L = aLWb	a = 0.967	0.989	$0 .967 (L_{1}^{} L_{2}^{} L_{3}^{} L_{4}^{} L_{5}^{} W)^{\frac{2}{6}}$
16.	A_L = aLb	a = 1.206	0.992	$1 .206 (L_{1}^{} L_{2}^{} L_{3}^{})^{0.630}$
17.	A_L = aLb	a = 0.933	0.969	$0 .933 (L_{1}^{} L_{2}^{} L_{3}^{})^{2 / 6}$
18.	A_L = aLWb	a = 1.465	0.994	$1 .465 (L_{1}^{} L_{2}^{} L_{3}^{} (0.5 W))^{0.467}$
19.	A_L = aLW2/4 + b	a = 1.063 b = 3.152	0.978	$1 .063 (L_{1}^{} L_{2}^{} L_{3}^{} (0.5 W))^{\frac{2}{4}} + 3 .152$
20.	A_L = aLWb	a = 1.103	0.976	$1 .103 (L_{1}^{} L_{2}^{} L_{3}^{} (0.5 W))^{\frac{2}{4}}$
*Note:* a and b are the equation coefficient, AL = Leaf area, L = rib length, W = width, P = leaf periphery.

Correlation with midrib length

Models No. 1, 2, and 3 showed the relationship between midrib length and leaf area with the corresponding coefficient of determination (0.985, 0.978, and 0.989), respectively. Model No. 1 had a quadratic form, while Model No. 3 was of power form. Since the area had the dimension of [L²], the relationship between the square of midrib length and leaf area was also worked out. The coefficient of determination for the power form equation was found to be the best.

Correlation with the product of rib lengths

Models 9 and 10 showed the relationship between the product of rib lengths (L₁.L₂.L₃.L₄.L₅) and leaf area. When the product of rib lengths was taken as an independent variable, a curvilinear relationship was observed with a coefficient of determination of 0.996. When the same equation was made dimensionally homogeneous by taking the 7^th root of the product of rib lengths and squaring after that, a higher coefficient of determination (0.986) was observed. Models 16 and 17 showed the relationship between leaf area and the product of rib lengths of half leaf (L₁. L₂. L₃). Model 17 was curvilinear with R² = 0.969, whereas Model 18 was linear with R² = 0.994.

Correlation with width, midrib length, and width

The correlation of leaf width with the area is depicted by models 4 and 5. Model 4 is nonlinear with R² = 0.987 and 5 is linear with R2 = 0.973. The linear model is a plot between the area and square width of the leaf, which is dimensionally homogeneous. Model 6 depicts the relationship between leaf area and the product of the midrib length (L₃) and width (W), which is dimensionally homogenous. The nature of the plot is linear, and the value of R² = 0.992. The value of R2 of Model 6 is superior to other models of L3 or W.

Correlation with the product of rib lengths and leaf periphery, rib lengths and width

Model 7 is dimensionally homogeneous showing variation of leaf area (L₁.L₂.L₃.L₄.L₅.P₁.P₂)0.274 with R² = 0.995. Model 7 is dimensionally non-homogeneous, and the plot is curvilinear with R² = 0.995. Model 7 seems superior over models 1-8 but requires a large number of linear measurements from a single leaf. Models 13, 14, and 15 show variation of leaf area with the product of rib lengths and width. Model 13 is nonlinear and dimensionally non-homogeneous with the value of R² = 0.997. Models 14 and 15 are dimensionally homogenous with R² = 0.990 and 0.989. Model 15 is passing through the origin, while model 14 has an intercept. Model 13 is superior to all the models discussed so far.

Correlation with the product of rib lengths, leaf periphery length, and width

Models 11 and 12 show the variation of leaf area with the product of rib lengths, perimetric base length, and width with R² = 0.996 and 0.993. Model 11 has a higher value of R² but without any further improvement in the coefficient of determination. Model 12 is dimensionally homogeneous. Both models require eight linear measurements for calculating leaf area without any modification.

Correlation with the product of half side rib lengths and half-width

Model 16 describes the variation of leaf area with the product of half side rib lengths (L₁.L₂.L₃) and dimensionally non-homogeneous, while model 17 is dimensionally homogeneous. The value of R² = 0.992 and 0.969 for models 16 and 17, respectively. Both the models are inferior to model 7. Model 18 is nonlinear dimensionally non-homogeneous with R² = 0.994, and models 19 and 20 are linear and dimensionally homogeneous with and without an intercept with corresponding R² = 0.978 and 0.976. These models are also not better performing than model 13. Model 13, having the highest value of R² =0.997 among all models and requiring only two linear measurements, midrib length (L3) and width (W), can be successfully used to calculate the leaf area of Jatropha curcas.

Discussion

Pompelli, et al [7]. Developed eight models for calculating leaf area using two linear leaf measurements: leaf length (midrib length) and width. All four models used the product of length and width for establishing the relationship with leaf area gave higher values of R2. Achten, et al [13]. Also recommended the calculation of leaf area with the help of leaf length and width. Severino, et al [24]. Also found that the leaf area calculated with the help of leaf length and width is superior to the leaf area calculated with the help of width alone [25-28].

Jatropha curcas leaf requires 18 linear measurements for fully describing the leaf. Measurement of leaf area of Jatropha is useful in understanding the physiological responses and yield productivity. The water requirements of the plant could also be correlated with the overall leaf area. Direct measurement of leaf requires expensive instruments, while allometric methods require a few leaf dimensions measurements. In the present study, relationships were developed for the calculation of leaf area of the Jatropha using leaf length (L), width (W), and/ or leaf periphery length (P). The models were evaluated based on the determination of coefficient (R²) and the difference between calculated and measured leaf area of Jatropha plant leaves. Accurate and simple equations were developed using leaf width (A_L = W^1.795), R² = 0.987, rib length (A_L = L₃^2.081), R² = 0.989, width and rib length (A_L = LW^0.320), R² = 0.997, rib length and leaf periphery segment (A_L= LP₁P₁₂^0.274), R² = 0.995, and half rib and width length (A_L = LW/0.5^0.467), R² = 0.994. The developed models calculated leaf area of small, medium, and large Jatropha curcas plants accurately and recommended for field application.

Acknowledgement

One of the authors, Krishan Kumar Verma is thankful to the Science & Engineering Research Board (SERB), New Delhi, India, for granting a Start-Up Research Grant Scheme -Young Scientist (F.No. SB/YS/LS-167/2013).

Authors’ contributions

KKV- conceived, designed, conducted the experiment, collected and analyzed data, wrote the manuscript, CLV- analyzed the mathematical model and MS- reviewed and approved the final version of the MS. All authors read and approved the final manuscript.