International Journal of Agricultural Science and Food Technology
Impact of row planting teff technology adoption on the income of smallholder farmers: The case of Hidabu Abote District, North Shoa Zone of Oromia Region, Ethiopia
Fekadu Adamu Negussie*
Cite this as
Negussie FA (2020) Impact of row planting teff technology adoption on the income of smallholder farmers: The case of Hidabu Abote District, North Shoa Zone of Oromia Region, Ethiopia. Int J Agric Sc Food Technol 6(2): 195-203. DOI: 10.17352/2455-815X.000074In Ethiopia, improved agricultural technologies, like row planting are promoted in the recent times in order to address low agricultural productivity. However, despite such production enhancing technologies, utilization of such technologies remained low in Ethiopia. This study is focusedon the impact of row planting teff technology adoption on the income of smallholder farmer in the context of Hidabu Abote District, North Shoa zone. The study uses cross-sectional data that were collected from 181 randomly selected smallholder farmers. The data were analyzed using descriptive, inferential statistics,and econometrics models. From the descriptive statistics, it was found that out of thirteen explanatory variables seven of them were a significant difference among the groups. Results of the probit model revealed that, distance to central market, extension contact,off/non-farm income,farm size,household size, access to mass media,and access to credit affected the farmer’s adoption decision of the row planting of teff significantly. The finding of the propensity score matching analysis revealed that the average teff income per hectare of adopter is greater than that of non-adopter. Therefore, the findings of the study safely recommended that those significant factors adoption decision of the row planting of teff by any development intervention and policy makers, should be considered in setting their policies and strategies to speed up the use of row planting of teff.
Introduction
The Sub Sahara African countries and Ethiopia specifically, is highly influenced by sustenance security issues because of the absence of receiving improved agricultural technologies. In Ethiopia, smallholder farmer’s production and profitability are tremendously low and the development of rural productivity has just barely kept rate with the development of the population. Still, the lack of agricultural technology practicing discourages farmers to improve productivity [1].
In Ethiopia, teff is one of the major crops widely produced much better than any other cereals by small-scale farmers. National Academy Science (1996) reported that, nutritionally, Teff has equal, or even more food quality than the other major grains: wheat, barley and maize. Teff grains contain 72.1-75.2% carbohydrate, 14-15% proteins, 11-33 mg iron, 100-150 mg calcium and rich in potassium and phosphorous. As indicated in the same report, the low level of anemia in Ethiopia seems to be associated with the level of Teff consumption as the grains contain high iron. Teff has got high lysine content compared to all cereals with the exception of rice and oats. It is highly adaptable to a wide range of soil types. It has the ability to perform well in black soils and, in some cases, in low soil acidities. In addition, teff has the capacity to withstand waterlogged, rainy conditions, often better than other cereal grains (other than rice) (ATA, 2013b).
Moreover, teff is the main crop of the country and stands first both in area coverage and production among cereals. For instance, the land covered by teff in 2016/2017 meher season is 24.00%; maize covered 16.98 %, sorghum 14.97 %, and wheat covered 13.49% of the total area covered by grain [2]. Teff has also the largest value in terms of both production and consumption in Ethiopia and the value of commercial surplus of teff is second only to coffee [3].
However, in spite of its economic importance and well adapted to growing environments in Ethiopia, the productivity of teff remains low [4]. In Ethiopia, the broadcasting method of teff planting used by the farmers is one of the main reasons why teff productivity is low [5]. It was also argued that the broadcasting method of teff planting reduces the productivity due to uneven distribution of seed increase competition between teff plant for nutrient, water, and light [6].
On the other hand, to alleviate this low production row planting technology with proper distance between crop rows was recommended in the country [7]. As past study result showed that the productivity of teff difference between the broadcasting and row planting of teff was 14.8 quintals per hectare and 20.1quintals per hectare respectively [8]. But, currently only a few farmers were using the row planting technology on their farming activity even though, teff research has received limited national and international attention, the latter presumably because of its localized importance in Ethiopia [6]. Moreover, teff productivity is low because of agronomic constraints that include lodging, low modern input use, and high post-harvest losses [6,9].
Actually, there are some findings focusing on impact and adoption of row planting technology of teff in Ethiopia. For instance; Behailu [10] studied on factors affecting farmers’ adoption level of row planting technology and yield improvement on the production of teff; Tadele studied on adoption and intensity of adoption of row planting of teff. The former studies focus only on adoption while the latter incorporates intensity of adoption and fills the gap of the former two findings. Moreover, only Amare Fantie (no date) and Yonas, B. [11] studied on the impact of row planting teff on the welfare of households at differet location. According to their study teff row planting technology had acceptable more teff crop yield and income than the broadcast planting method. Though, there is lack of more empirical knowledge on the impact of manual teff row planting on on teff crop income per hectare in the country. Following the above gap, before studying the farmer’s intensity of adoption and continued application of farmers the impact of row planting technology of teff by smallholder farmers in the study area is necessarily investigated.
Hidabu Abote District is one of the areas in North Shoa zone of Oromia region,Ethiopia. Most of the farmers in the area are rural and highly produce teff for their consumption purpose and as sources of income. But, the teff productivity could not reach its required level. The method of teff planting which is practiced in the area is teff broadcasting. This is one of the major problem farmers to increase their teff productivity. Moreover, as far as the knowledge of the researcher concerned there was gap of study particularly in the study area. Some earlier findings were studied at national, regional and/or zonal level. While an investigation on location-specific regarding appropriate agricultural technology is essential to improve the adoption system and to support the assumption on adoption decision. Consequently, this investigation was initiated to fill the gap of the farmer’s adoption decision and the impact of row planting of teff on smallholder farmer’s teff income per hectare in the case of study area.
Objectives of the study
The general objective of this study was to assess the impact of row planting technology adoption on teff crop income of smallholder farmers in the case of Hidabu Abote District.
To identify factors affecting the adoption decision of row planting technology of teff.
To analyze the impact of row planting technology adoption on teff crop income per hectare.
Methodology
Description of thestudy area
Hidabu Abote District is one of the 13 district in North Showa Zone known for predominantly growing teff. It is located, north of Dera District, South of Degem, East of Degem, and West of Wara Jarso District. Hidabu Abote District with the capital Ejere town has a total area of 454km2 and about 42 km from the town of North Shoa (Fitche) and 147km from Addis Ababa.The total area of the district is 48,600 hectare from this 32,917 hectareis used for agricultural land. The woreda is known by high potential area for teff production. There are 19 kebeles and 1 urban kebeles. The number of agricultural households in the district was 20,406, from this (18,000) male headed (89%) and 2400 female-headed (11%), while the total population of the district was 104,442 from which 51,030 are males and 53,412 females.Geographically Hidabu Abote District extends from 9047’- 10011’north latitudes and 38027-38043’ east longitudes (HADAO, 2018).
The average annual rainfall of the district is 800 mm-1200mm with low variability. It is bimodality distributed in which the small rains are from March to April and the main rainy season from July to September. Hence, crop and livestock production is not constrained by the distribution of rainfall. Altitude in district ranges from 1160m to 3000m above sea level (masl). The temperature of the district is minimum130c and maximum 200c. The soil types of the area is sandy soil 14%, clay soil 51%, and silt 35%.The agro-climate/ecological zone of the area is, highland 6%, mid-altitude 50%, and lowland 44%.
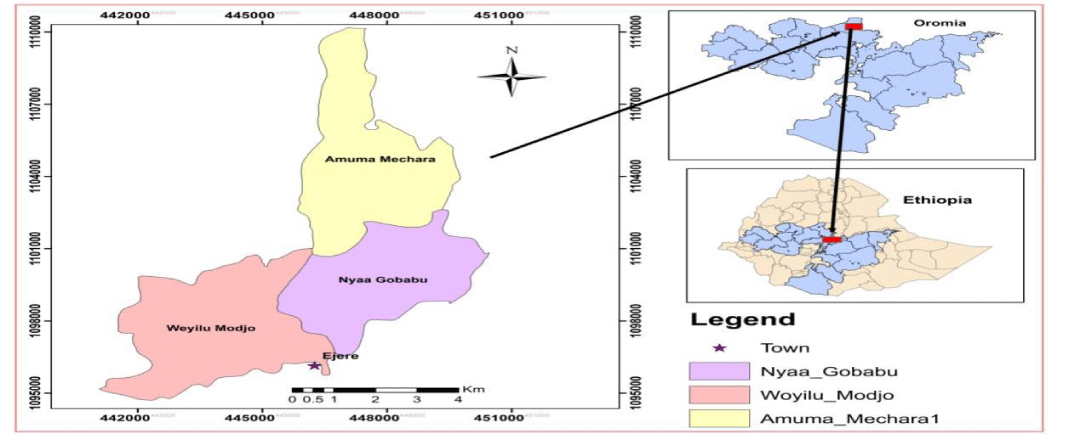
In the study area agriculture contributes much to meet major objectives of farmers such as food supplies and cash needs. The sector is characterized by it is rain-fed and subsistence nature. It is the mixed farming type where crop and livestock productions are undertaken side by side.Hidabu Abote is one of the potential teff producing district in Oromia region and ranked the 5thfrom top 25 teff producing district at the national level, and it ranked to the 4thin Oromia region and the 1st in North Shoa administrative zone. Furthermore, teff is the major crop produced in mid-altitude area in the district and which is the major source of income for households Figure 1.
Sampling methods and sample size determination
The data used in this study consists of household sample survey data collected in the rural area of Hidabu Abote District in North Shoa zone. The multi-stage sampling technique was employed to select the sample respondent. In first stage, Hidabu Abote District has three agro-ecological zones: lowland, mid-altitude, highland. The dominant teff producing agro-ecological zone is mostly mid-altitude area. Hence, the target farming households are from this area. Out of the total kebeles found in mid-altitude agro ecology of the district the potential teff producing kebeles were identified. Hence, these kebeles have both households practicing the row planting with improved teff seed and those practices broadcasting planting method with improved teff seed.
In the second stage,based on time, accessibility, and considering how well the sample size is representative, three kebeles were selected by using a random sampling technique. Moreover, selection of the three kebeles is also possible because of the total distributions of the farm households of the area are socioeconomically, culturally and institutionally similar for the potential teff producer kebeles in the district. Moreover, the administration, technology diffusion procedures and plans of development by the leaders are almost the same for these selected kebeles and so any household from any kebeles can be representative of each other.Then, the farmers in each randomly selected kebeles were stratified into adopter and non-adopter categories giving the relative homogeneity of sample respondents’ adoption status. Due to heterogeneity of the population the sample size was determined using the formula developed by Cochran’s [12].
Where n is the sample size for the study, z is the selected critical value of desired confidence level which is 1.96; p is the estimated proportion of an adopters of row planting teff attribute that is present in the population of teff potential producers in the district which is 0.36, q=1-p =0.64 and due to heterogeneous characteristics of the farmers the precision level e value of 0.07 was used. In the final stage, farm households consisting of 72 row planting adopters and 109 non-adopters were selected from the identified list using simple random sampling technique taking into account probability proportional to size of the identified households in each of the three selected kebeles.
Method of data collections and methods of data analysis
The research design that was used in this study is the cross-sectional design. Both primary and secondary data were used for this study. Primary data was collected with the help of the survey by means of the structured interview schedule for the quantitative data. After coding and feeding the collected primary data into the computer, STATA version 13.0mp software packagewas employed for the analysis. The data were analyzed using descriptive statistics, inferential statistics and econometric models.
Econometric models
Determinants of the farmer’s adoption decision of the row planting of teff crop technology: Binarydependent variable models have been widely used in technology adoption studies. Logit and probit models are the convenient functional forms for models with binary dependent variables [13]. These two models are commonly used in studies involving qualitative choices. The logit model uses the cumulative logistic function. But this is not the only cumulative distribution function that one can use. In some applications the normal cumulative distribution function has been found useful. The estimating model that emerges fromnormal cumulative distribution function is popularly known as the probit model [14]. For this study a probit model selected over the logit, because the dependent variable has a latent observable value.
Specification of econometric model
By following Feleke and Zegeye [15], Janvry, et al. [16], and Kohansal andFiroozzare [17], Ghimire, et al. [18], the adoption decision can bemodeled in a random utility framework as follows:
Where, is the latent variable which represents the probability of household’s decision to adopt the row planting of teff, takes the value ‘1’ and ‘0’ otherwise. In the analysis a probit equation was specified for weather or not the household participating in the row planting of teff technology. The term Xi represents explanatory variables explaining the adoption decision, y is a vector parameters to be estimated, and uiis the error term assumed to be independent and normally distributes as ui~ N (0, 1).
Where is a latent variable that takes the value 1 if the farmer adopt the row planting of teff technology (Ui=1) and zero otherwise, Ui=1 is the observed variable which represent farmers adoption of the row planting technology of teff, X-is a vector of explanatory variables hypothesized to influence the decision to use, y-is a vector of parameters and µi-is error term.
The probit model for the analysis of Ui is (1, 0) where the information on the latent variable is only observed through the index function. The probability that a farmer will adopt the modern row planting is a function of the vector of explanatory variables and the unobserved error term. As the form of is not known, we assume to have a cumulative normal distribution on the assumption that µi has a normal distribution.In this study a probit model was employed todetermine the probability of adoption decision the row planting of teff using a cross sectional survey data. Therefore, in present study the estimated themarginal effect of independent variables in the probitmodel which can be obtained by differentiating thefirst and second order conditions as follows [19]:
Prior to running the probit model, an assessment for an existence of multicollinearity was checked. Accordingly, a separate test for continuous and dummy variables included in the model was undertaken using VIF and contingency coefficient (CC) procedures respectively. VIF test was used to detect the presence of multicollinearity problem among continuous dependent variables. Accordinglly, VIF can be computed by using the formula: Where,R2 is the multiple correlations between Xi and others explanatory variables. As a rule of thumb a VIF value of more than 10 indicates high correlation among explanatory variables, while a VIF value less than 10 indicates weak association among explanatory variables [14]. Similarly, the existence of association among discrete explanatory variables was tested using contingency coefficient method by using the formula.
A value of 0.75 or more indicates stronger associations while a value less than 0.75 indicates weak association among explanatory variables. Additionally, an assessment for an existence of Heteroskedasticity was checked. Heteroskedasticity occurs when the variance of the error term is not consistent, Leading to the inefficient and invalid test of hypothesis [5]. If present in the data the estimates will not be the best linear unbiased estimates (BLUE). In this study, the Breusch-Pagan/Cook Weisbergi test was used to test for heteroskedasticity under the null hypothesis of a constant variance. In this study, A goodness of fit value was estimated. A goodness of fit measure is a statistic showing the accuracy with which a model approximates the observed data. To measure the goodness of fit in the qualitative model Greene (2003) suggests the use of the LR. The LR is also called McFadden R2or pseudo R2 and is analogous to R2 in a regression (ibid).
Where Lnl is the independent variables log-likelihood function for the model with all the independent variable and Ln0 is the log-likelihood computed with the constant term only.
Estimated result of the impacts of row planting of teff technology adoption
Propensity score matching method: Due to the absence of panel data, this study employs statistical matching to address the problem of selection bias. This involves pairing adopters and non-adopters that are similar in terms of their observable characteristics [20]. When outcomes are independent of assignment to treatment, conditional on pretreatment covariates, matching methods can yield an unbiased estimate of the treatment impact. In a study by Michalopoulos, et al. [21] to assess which non-experimental method provides the most accurate estimates in the absence of random assignment, they conclude that propensity score methods provided a specification check that tended to eliminate biases that were larger than average. On the other hand, the fixed effects model did not consistently improve the results. Therefore, in this study propensity score matching model was used.
Based on Rosenbaum and Rubin [22], propensity score can be defined as the conditional probability of receiving a treatment given pretreatment characteristics. Therefore, Let YiT and YiC are the outcome variable for participant (row planting) and non-participant (broadcast), respectively. The difference in outcome between treated and control groups can be seen from the following mathematical equation:
Where, YiT : Outcome of treatment (teff crop income per hectare of the ith household, when he/she is participant), YiC : Outcome of the non-participant individuals (i.e Teff crop income per hectare of the ith household when he/she is non participant in teff row planting), ∆i: is change in the outcome as a result of teff row planting for the ith household. Let the above equation be expressed in causal effect notational form, by assigning Di=1 as a treatment variable taking the value 1 if the individual received the treatment (row planting) and 0 otherwise. Then the Average Treatment Effect of an individual i can be written as: ;Where ATE, average treatment effect, which is the effect of treatment on the outcome variable: E(YiT/Di=1): Average outcomes for individual, with treatment, if he/she would participant (Di=1). E(YiC/Di=0): Average outcome of untreated, when he/she would non-participant, or absence of treatment (Di=0).
The average effect of treatment on the treated (ATT) for the sample households is given by: . The fundamental evaluation problem in estimation of impact is that it is impossible to observe a person’s outcome for with and without treatment at the same time. While the post-intervention outcome E(YiT/Di=1) is possible to observe, however, the counterfactual outcome of the ith household when she/he does not use the treatment is not observable in the data. Thus, estimation of ATE can give a seriously biased result, due to the fact that the population can differ among the comparison group, not only in terms of treatment status, but even in terms of other characteristics: this problem is often referred to as the “fundamental problem of causal inference’’. Thus, simple mean comparison between the treated and non-treated can be misleading, yet taking the mean outcome of non-participants as an approximation is not advisable, since participants and non-participants usually differ even in the absence of treatment [23]. A solution to this problem is to construct the unobserved outcome which is called the counterfactual outcome that households would have experienced, on average, had they not participated (Rosenbaum and Rubin, 1983) [22], and this is the central idea of matching. According to Rosenbaum and Rubin [22], the effectiveness of matching estimators as a feasible estimator for impact evaluation depends on two fundamental assumptions, namely: Assumption 1: Conditional Independence Assumption (CIA): It states that treatment assignment (Di) conditional on attributes, X is independent of the post program outcome (YiT ,YiC ). In formal notation, this assumption corresponds to: .
Assumption 2: Assumption of common support: 0 Participation on training: The result indicated that out of the total sample respondents 47.2% of the adopters and only 9.1% of non-adopters have participated in training. Moreover, 52.8% of the adopters and 90.9% of the non-adopters did not involve on training trial on the same year. The percentage difference between the groups related to this variable was found to be statistically significant at P<.01 level of significance. Access to mass media: The result of chi-square value indicated there is statistically significance difference between the adopters and non-adopters of row planting of teff at P<.01 level of significance. Moreover, 72.2% of adopters and 53.6% of non-adopters were use different mass media sources while, 27.8% of adopters and 46.4% of non-adopters were not have the access mass media. Access to credit service: as result shows 56.9% of adopters and 47.3 of non-adopters were access the credit while 43.1% of adopters and 52.7% of nonadopters were not access to the credit. Therefore, the chi-square analysis result revealed that access to credit service shows statistically significant association with the adoption decision with at P<.01 level of significance. Access to improved teff seed: The study result indicated that 88.9% of adopters and 54.5% of non-adopters of row planting were adequate to improved teff seed during the teff production while 11.1% the adopters and 45.5% non-adopters were not adequate of the improved teff seed during teff production. The chi-square analysis result revealed that the percentage difference between the groups is significant at P<.01 level. Household size:. In this study, the mean adult equivalents of sample adopters and non-adopters households were 4.66 and 3.83 adult equivalent with a standard deviation of 1.28 and .833 respectively. Hence, household size in adult equivalent shows that there is a statistically significant mean difference between both adopters’ categories at P<.01 significant level. The education level: The result shows that the mean educational level of household adopters of row planting was 2.38 years with the standard deviations of 2.96 where as the mean educational level of non-adopters were 1.83 years with standard deviation of 2.56. An independent sample t-test results showed that there is a statistically significant mean difference between adopters and non-adopters farmers in terms of the educational level at p<.1 level of significance. Extension contact: The average extension contact of adopters was 3.93per month with the standard deviation of 1.43 while that of non-adopters was 2.43 with the standard deviation of .99 per month of the same year. This study identified that, the mean difference between the groups related to frequencies of extension contact as statistically significant between adopters and non-adopters at P<.01significance level. Determinants of the farmer’s adoption decision of the row planting of teff technology: The probit model was employed to identify factors affecting the adoption decision of the row planting technology of teff. A total of thirteen explanatory variables, of which eight were continuous andfive were dummy variables, were included in the model. The model wald-Chi-square test value of 199.86 and is significant at 0.000. It has a log likelihood value of -22.22678. The probability of getting the wald Chi-square teststatistic (Prob> chi2) extreme than the null hypothesis was 0.000. Thus, testing at 0.05 then 0.000 <0.05 which leads us not to accept the null hypothesis that all the regression coefficients in the model are equal to zero. The Count R2 was 0.81. This shows that 81% of the variation in the adoption decision was explained by the variation in the explanatory variables. Marginal effects in probit coefficients: The probit coefficients give the predicted probability. The coefficients cannot be interpreted directly without further calculation as suggested by Greene [19]. Therefore, in order to know the amount of change in probability due to a unit change in the explanatory variable, marginal effects were used. Marginal effects were calculated by taking commands for adoption probability. Distance to the centeral market: Market distance has negative relation and significantly affected at P< .1 significance level on the adoption of row planting technology as indicated in Table 2. Hence, the result of the marginal effect explains that if the distance between farmers and market increase the probability in favor of the change of the farmers of marginal adoption of teff production technology is decreased by 20.6%. Access tomass media: Access to mass media is positively influencing the adoption decision of row planting of teff at P< .01 level of significance. It is important to make farmers aware of new agricultural innovation to proceed for the next step of weighing the advantage and limitation of the technology. Hence, the result of the marginal effect explains that if households has access to mass media in favor of the change of the farmers of marginal adoption of teff production technology is increased by 32%. Extension contact: This variable has an important factor on the teff production technology adoption decision and the result was significant at P< .01 significance level. Other variables held constant, for each additional contact with agricultural extension agents the probability of adoption decision of teff row plant technology increases by 21%. Off/non-farm income: According to the finding of the study revealed in Table 2 off/non-farm income is statistically and positively significant which affect farmers’ adoption decision towards row planting technology of teff at P< .05 level of probability. Other variable constant, an increase the off/on farm income the change of the probability of the farmers to use row planting technology of teff is increased by 0.006%. Farm size: This variable positively influences the adoption decision of farmer’s the row planting technology of teff. It is significant at P< .1 probability level. Keeping the effects of other variables constant, the marginal effect indicated that as increase the land size of the farmers by one hectare the probability of the farmers adoption decision of the row planting technology is increased by 25.5%. Household size: Family labor in adult equivalent was positively and significantly influenced the adoption decision of row planting of teff at P< .01 probability level. Keeping all other variables constant, a unit increase in family labor, increases the use of row planting technology of teff by 29.4%. Access to credit service: - It is also significantly influencing the use of row planting of teff production package at P< .05 level of significance. The marginal effect of probit model result indicated that, if the household heads had accessto credit, the probability change of farmer’s adoption decision in favor of households’ use of row planting teff production is increased by 36.4%. The study provided evidences as to compare whether or not application of row planting of teff technology brought a significant impact on the teff income per hectare of rural farming households. The logistic regression model was used to estimate propensity score for adopters and non-adopters of the technology. A result presented after matching shows the estimated model appears to perform well for the intended matching exercise. The pseudo-R2 value is 0.35, a low R2 value shows that teff farming households do not have much distinct characteristics overall and as such a good match between adopters and non adopters of technology becomes easier.The objective of matching procedure is to get similar probability of adopting or not adopting the technology under consideration within a given explanatory variables.The evaluator is guided by economic theory and empirical studies to know which observables affect both participation and the outcomes of interest [24]. Hence, implementing matching requires choosing a set of variables X that credibly satisfy this condition. After estimating the propensity score, the next step is to verify the quality of the match by controlling the region of common support between the treatment and control group. In practice, all those treatment observations were deleted whose propensity score is smaller than the minimum and higher than the maximum propensity score of the control group Table 3. The predicted propensity scores range from .0553659 to .9968217 with mean value of .6418209 of the row planting teff farmers, while it ranges from .0019935 to .8745162 with mean value of .2344445 for those non-row planting teff farmers. Accordingly, the common support region was satisfied in the range of [.0553659 to .874516] with only 25 losses of observations (19 from non –adopters and only 6 losses from adopters of row planting of teff farmers). Accordingly, 66 households from the adopters and 90 households from non-adopters groups satisfy the common support condition. The main purpose of the propensity score estimation was to balance the observed distributions of covariates across two farmer groups. Alternative matching estimators can be employed in matching the treatment and comparison groups in the common support region. The final choice of a matching estimator can be done by taking selection criterion either of balancing test, pseudo-R2, and matched sample size. Accordingly, a matching estimator which balances all explanatory variables, a model which bears a low pseudo R2 value and results in large matched sample size is a preferable matching algorism [20]. Therefore, for this study the kernel matching that matches a treated unit to all control units weighted in proportion to the closeness between the treated unit and the control unitwas employed. Balancing test conducted to know whether there is a statistical significant difference in the mean values of covariates adopters and non-adopters of technology. The higher the covariates with minimum mean difference after matching is the more balanced covariates. Keeping other selection criterion, the balancing test indicates the quality of the matching algorithm implemented. While evaluating treatment effect, the major econometric problem is selection bias as stated in Maddala [25], percentage of bias before matching is in the range of 9.1% and 87.1% while after matching, percentage bias lies between 1.9% and 16.9%, which is below the critical level of 20%. In all cases, it is evident that sample differences in the unmatched data significantly exceed those in the samples of matched cases. The process of matching thus creates a high degree of covariate balance between the treatment and control samples that are ready to use in the estimation procedure. In a similar approach, t-tests could have been conducted to verify the equality of means for both the treatment and the control group. Differences in means before matching are natural, but after matching there should not be significant differences in the means as the covariates should be balanced satisfyingly. Similarly, t-values show that before matching seven of chosen variables exhibited statistically significant differences while after matching all of the covariates are balanced. As data result also revealed in the balancing test, the covariate balancing after matching indicates the low pseudo R2 and insignificant p-value of the likelihood ratio test supports the hypothesis that row planting and broadcasting teff farm households have the same distribution in covariates after matching. These balancing test results are used to measure the impact of row planting technology of teff among groups of households having similar observed characteristics. The impact of row planting technology of teff producing farming household’s teff income per hectare is estimated using kernel band width (0.25) matching and ATT is compared among these algorithms. The matching techniques are kernel neighbour matching. The matching algorithms showed that the adopters of the row planting of teff technology had a positive and significant effect on teff income per hectare. The following result showed that the estimation of average treatment effects on the treated (ATT) from the kernel band width (0.25) matching algorithms. From the Table 4 above, it is identified that the average treatment effect on the treated of teff income is 9748.73415 Ethiopian Birr per hectare with t-value 10.81 for kernel matching indicating the effective level of significance.Therefore, in present study, the result revealed that the row planting teff adoption has positive effect on teff income per hectare of stallholder farming households of the study area. There may be hidden biases against the result of matching estimators and hence testing robustness the result is recommended. As it is not possible to estimate the magnitude of the selection bias with non-experimental data, the problem can be addressed through using sensitivity test. The basic issue in testing sensitivity is to check whether the treatment effect is due to unobserved factor or not. Rosenbaum [22] proposes using Rosenbaum bounding approach in order to check the sensitivity of the estimated ATT. The results shows that the impact of the technology intervention is not changing through adopter and non-adopter households if it is allowed to differ odds of being treated up to Gamma=2. That means for the outcome variable estimated, at various level of critical value of gamma, the p-critical values are significant which further indicate that consideration of important covariates that affected both adoption and outcome variables. The study didn’t get the critical value gamma where the estimated ATT is questioned even if the set gamma largely up to 3, which is larger value, compared to the value set in different a literature which is usually 2 (100%). Thus, it can be concluded that the impact estimates (ATT) are insensitive to unobserved selection bias and are a pure effect of income due to technology adoption [26-33].
Based on the study findings, the following recommendations are drawn that should be taken in to consideration by respective government bodies in the study area. The result of the study revealed that distance to central market was statically significant and negatively affected the adoption decision of the row planting of teff technology. Consequently, the government’s bodies need to establish market center for the farmers around their home with increase the probability of adoption of row planting of teff. The result of the study also identified that extension contact and access to mass media is positively and significantly influenced the farmers adoption decision of the row planting of teff technology attention had better necessary on which organizing farmers to share and discuss ideas from different mass media sources like, radio with their own local development group is important to fill the available information gaps. Additionally, extension service need to be done by the woreda agricultural extension office to update the theoretical and practical knowledge of the extension personnel about recently developed row planting technology. Moreover, the findings of the study revealed that access to credit service and house hold size is positively and significantly affected the farmers’ adoption decision of the row planting technology of teff. Thus, policy makers and bankers had better to provide loans to smallholders teff farmers and ensure a high rate of loan recovery and low cost of credit. Farmers had better also encouraged forming their own savings and credit cooperatives at the rural community level. Furthermore, row planting technology of teff is labor intensive mostly at the time of sowing. Therefore, any development intervention had better provide a row planter machine which substitute human labor and compatible to the given environment. Finally,the finding of the PSM model revealed that the adoption of row planting teff technology has a positive impact on teff income per hectare of smallholder farming households.The implication of the findings is straight forward; though the adoption of improved teff technologies is quite low in the study area. Hence, scaling up the best practices of the adopters toother farmers can be considered as one option to enhance teff productivity in the area while introducing new practices and technologies which save time and labor cost is another option. As a result, scaling up and diffusion of the technology in the study area should be highly recommended.Results and discussion
Study result of descriptive statistics
Econometric result
Propensity score matching result
Choice of matching algorithm and matching
Testing the balancing properties and covariates
Estimation of treatment effect
Sensitivity analysis
Conclusions and recommendations
- Aseyehegn K, Yirga C, Sundar R (2012) Effect of small scale irrigation on the income of rural farm households. The case of LaelayMaichew distinct, central Tigray, Ethiopia. Journal of Agricultural Sciences 7: 43-57. Link: https://bit.ly/3jLwGKm
- CSA (Central Statistics Agency) 2016-17, Agricultural Sample Survey: Area Planned and Production of Major Grains, private peasant holdings, Private Peasant Holdings, Meher season; April, 2017, Addis Ababa, Ethiopia.
- Minten B, Tamru S, Engida E, Kumar T (2013) Ethiopia’s Value Chains on the Move: The Case of Teff. ESSP II Working Paper 52. International Food Policy Research Institute (IFPRI). Addis Ababa, Ethiopia. Link: https://bit.ly/3kJU3Fr
- Abraha MT, Shimelis H, Laing M, Assefa K (2016) Achievement and gaps in teffproductivity improvement practices in the marginal areas of Northern Ethiopia: Implications for future research directions. International Journal of Agricultural Sustainability 15: 42-53. Link: https://bit.ly/3e9YVl0
- Wooldridge JM (2003) Further results on instrumental variables estimation of average treatment effects in the correlated random coefficient model. Economics Letters 79: 185-191. Link: https://bit.ly/34HdLvZ
- Fufa BB, Simons BR, Berhe T (2011) Tef Diagnostic Report: Strengthening theTef Value Chain in Ethiopia. Addis Ababa, Ethiopia.
- Alemo T, Emana B, Legesse B (2014) Impact of Wheat Row Planting on Yield of Smallholders in Selected Highland and Lowland Areas of Ethiopia. Al International Journal of Agriculture and Forestry 4: 386-393.Link: https://bit.ly/3oFL5eR
- Tesfaye W, Abdissa T, Yadessa GB (2015) Economic analysis of tef yield response to different sowing methods: Experience from Illuababora Zone, Ethiopia. Journal of Economics and Sustainable Development 6: 56-61. Link: https://bit.ly/3eatneR
- Habtegebrial K, Singh BR, Haile M (2007) Impact of tillage and nitrogen fertilization on yield, nitrogen use efficiency of tef (Eragrostistef (Zucc.) Trotter) and soil properties. Soil and Tillage Research 94: 55-63. Link: https://bit.ly/2HUy14g
- Behailu G (2014) Assessment of Factors Affecting Farmers’ Adoption level of Row Planting Technology and Yield Improvement on the Production of Eragrostis Teff [ZUCC.]: The Case of Minjar Shenkora Woreda, Amhara Region, Ethiopia (Doctoral dissertation, Addis Ababa University). Link: https://bit.ly/3jK3mnB
- Yonas B (2006) The impact of row planting of teff crop on rural Household income: A case of Tahtay Maychewwereda, Tigrai, Ethiopia (Doctoral dissertation, Mekelle University). Link: https://bit.ly/2HQ3Trk
- Cochran WG (1977) Sampling Techniques. 3rd ed. New York:John Wiley and Sons. Link: https://bit.ly/38anygz
- Johnston J, Dandiro D (1997) Econometric Methods.4th Ed. New York, McGraw-Hill Companies, Inc.
- Gujarati DN (2004) Basic econometrics 4th edition. India, New Delhi, Tata McGraw-Hill Publishing company
- Feleke S, Zegeye T (2006) Adoption of improved maize varieties in Southern Ethiopia: Factors and strategy options. Food Policy 31: 442-457. Link: https://bit.ly/3kKUI9T
- Janvry DA, Dustan A, Sadoulet E (2010) Recent advances in impact analysis methods for ex-post impact assessments of agricultural technology: Options for the CGIAR. In: Proceeding of University of California at Berkeley. http://impact cigar org/meetings-and events. Link: https://bit.ly/3edqGch
- Kohansal MR, Firoozzare A (2013) Applying multinomial logit model for determining Socio-economic factors affecting major choice of consumers in food purchasing: The case of Mashhad. J Agric Sci Technol 15: 1307–1317. Link: https://bit.ly/3oIvo6N
- Ghimire R, Wen-chi H, Shrestha RB (2015) Factors affecting adoption of improved Rice varieties among rural farm households in Central Nepal. Rice Science 22: 35-43. Link: https://bit.ly/3mGw0rU
- Greene WH (2012) Econometric analysis 7th edition. USA, Pearson education, Inc. Link: https://bit.ly/3oKmGVu
- Dehejia RH, Wahba S (2002) Propensity score matching methods for non- experimental causal studies. The Review of Economics and Statistics 84: 151-161. Link: https://bit.ly/31ZR707
- Michalopoulos C, Bloom HS, Hill CJ (2004) Can propensity-score methods match the findings from a random assignment evaluation of mandatory welfare-to-work programs? Review of Economics and Statistics 86: 156-179. Link: https://bit.ly/3ebL3Xn
- Rosenbaum PR, Rubin DB (1983) The central role of the propensity score in observational studies for causal effects. Biometrika 70: 41-55. Link: https://bit.ly/34J1qHZ
- Caliendo M, Kopeinig S (2008) Some practical guidance for the implementation of Propensity score matching. Journal of Economic Surveys 22: 31-72. Link: https://bit.ly/2HUfHs3
- Bryson A, Dorsett R, Purdon S (2002) The use of Propensity Score Matching in the Evaluation of Labor Market Policies. Link: https://bit.ly/37Yo6pG
- Maddala GS (1997) Limited dependent and qualitative variables in Econometrics. Cambridge University press
- Bekele A, Kassa B, Legesse B, Lemma T (2011) Effects of crop commercial orientation on productivity of smallholder farmers in drought-prone areas of the Central Rift Valley of Ethiopia. Ethiopian Journal of Agricultural Sciences 21: 16-34. Link: https://bit.ly/34Kkp4N
- Fentie A (2017) Measuring the Impact of Row Planting Agricultural Technology Adoption the Welfare of Rural Small Holders.
- Gujarati DN (2003) Basic Econometrics, 4th Edition. McGraw-Hill, New York 563-636.
- Beshir H (2014) Factors affecting adoption and intensity of use of improved forages in North East Highlands of Ethiopia. American Journal of Experimental Agriculture 4: 12-27. Link: https://bit.ly/2TJ5Gk4
- James HJ, Ichimura H, Todd P (1998) Matching as an Econometric Evaluation Estimator, Review of Economic Studies 65: 261-294. Link: https://bit.ly/3eePYXn
- Kassie M, Zikhali P, Pender J, Köhlin G (2010) The economics of sustainable land management practices in the Ethiopian highlands. Journal of Agricultural Economics 61: 605-627. Link: https://bit.ly/384tmb0
- Vandercasteelen J, Dereje M, Minten B, Taffesse A (2016) Row planting teff in Ethiopia: Impact on farm-level profitability and labor Allocation. ESSP II Working Paper 92. Washington, D.C. and Addis Ababa, Ethiopia: International Food Policy Research Institute (IFPRI) and Ethiopian Development Research Institute. Link: https://bit.ly/2HPt6lG
- Smith and Todd (2005) Practical propensity score matching: Department of Economics and SIPA, Columbia University.
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.

 Save to Mendeley
Save to Mendeley
