Hedging policy using neural networks and its combination with heuristic algorithms case study: Dez Reservoir

In recent years, the use of various Artificial Intelligence (AI) methods, such as evolutionary computation, heuristic algorithms, artificial neural networks, and fuzzy theory calculations, has gained popularity in addressing water resources issues. These algorithms have shown great success in solving problems that traditional deterministic methods struggle with. This study focuses on optimizing Dez reservoir operation over a long-term period using a nonlinear loss function through an evolutionary artificial neural network algorithm. The outcomes of this approach are then contrasted with genetic exploration and harmony search algorithms, highlighting the strengths and weaknesses of each method. Ultimately, a combination of the evolutionary artificial neural network method and hedging models is employed for optimal reservoir management, with results compared to the previous approach. Results show the appropriate performance of combining hedging policy with artificial neural network and harmony search algorithm. This combination significantly reduces the vulnerability value with a slight decrease in reliability.

Introduction

Water operation managers use hedging policies to minimize water usage and safeguard it for the future. The aim of the hedging policy is to minimize vulnerability. The annual peak vulnerability represents the highest deficit experienced throughout the simulation period. A lower value indicates fewer significant system failures. Given the non-linear relationship between the loss function and shortage levels, decreasing the severity of shortages will lead to cost savings. Bower, et al. were pioneers in studying the economics of hedging policies [1]. Subsequently, other researchers such as Klemes [2], Stedinger [3] and Loucks, et al. [4] explored the optimization of planning and management objectives in various approaches. Hashimoto, et al. [5] introduced the initial hedging policy. Bayazit and Unal [6] revisited the topic of hedging and analyzed how to establish hedging parameters in reservoir development. Subsequently, Shih and Revelle [7,8] proposed the single-point and the discrete hedging approaches. After that, different solution methods were invented to obtain the decision variables of these policies. One of these methods is artificial neural networks and evolutionary algorithms.

The brain's learning and training mechanism relies on experience. Electronic models of natural neural networks also follow this principle, approaching problems differently from traditional computer calculation methods. The basic artificial neural network model faced a setback in solving nonlinear problems. However, multilayer networks and feedback-learning algorithms can address these issues. At that time, recurrent networks and the Hebbian learning method were introduced [9]. The application of neural networks in various aspects of water resources management, such as rainfall and runoff models [10], rainfall prediction [11], groundwater issues [12], irrigation tanks [13] and reservoir operation rule curves [14,15], expanded rapidly. In traditional neural network training, a dataset of input and output patterns is required. However, this training process and data utilization do not ensure the most optimal solution. Consequently, alternative optimization methods were employed to train the neural network model. For instance, Chandramouli and Raman [16], trained the neural network using outcomes from dynamic programming and implemented it for single and multi-reservoir operation rule curves.

Chang, et al. [17] employed the genetic algorithm to discover the optimal reservoir operation rule curve. In 2008, Chavez and Chang [18] utilized a neural network trained by Genetic Algorithm (GA) for a multi-purpose reservoir system. In 2011, Pianosi, et al. [19] utilized a combination of artificial neural networks and multi-purpose genetic algorithms for integrated reservoir operation. These methods are referred to as evolutionary neural networks.

Among various heuristic algorithms, genetic algorithms have been extensively utilized in solving water resource optimization problems in recent years. The genetic algorithm functions as a general search method that mimics the principles of natural biological evolution. Initially introduced by Holland [20], this algorithm has evolved into a potent optimization tool. Subsequently, numerous studies have explored the application of genetic algorithms in diverse optimization resource challenges. For instance, Esat and Hall [21] employed the genetic algorithm to determine the optimal path in a four-reservoir system, aiming to generate electricity and fulfill agricultural requirements. Oliveira and Louks [22] utilized the genetic algorithm with real numbers to ascertain the optimal curves for reservoir utilization. Wardlaw and Sharif [23] compared the genetic algorithm's performance in binary mode and real numbers, while Sharif and Wardlaw [24] applied this algorithm in a multi-reservoir system in Indonesia to analyze reservoir development scenarios. In recent times, genetic algorithms have been instrumental in resolving various water resources management optimization problems. For further exploration and research in this domain, refer to Nicklow, et al. [25].

Although heuristic algorithms are inspired by natural phenomena, there are also algorithms that are imitated by artificial phenomena in their creation. Among the recent algorithms, we can mention the harmony search algorithm (HS) that was invented by Geem, et al. [26] based on the artificial phenomenon of "musical harmony". "Harmony" in nature is a special relationship between several sound waves that have different frequencies. After that, Mahdavi, et al. [27] applied changes in the harmony search algorithm and called it the modified harmony search algorithm. Omran and Mahdavi [28] created a new algorithm by making a change in the original algorithm. Based on the initial algorithm, Pan, et al. [29,30] invented a harmony search algorithm with a set of parameters and a self-adaptive harmony search algorithm.

In this study, the optimization of Dez reservoir operation over a long-term period is examined using a nonlinear loss function through the evolutionary artificial neural network algorithm. Subsequently, the outcomes derived from this approach are contrasted with those from genetic exploration and harmony search algorithms, highlighting the advantages and limitations of each technique. To enhance reservoir management, a hybrid approach combining the evolutionary artificial neural network method with hedging models is implemented and its outcomes are evaluated against the initial state.

Methodology

Hedging policy

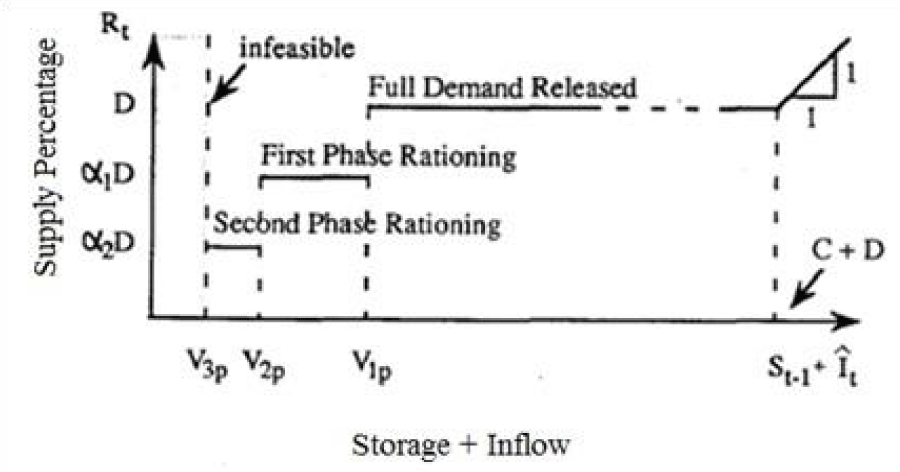
Water operation managers use hedging policies to minimize water usage and safeguard it for the future. The aim of the hedging policy is to minimize vulnerability. The annual peak vulnerability represents the highest deficit experienced throughout the simulation period. A lower value indicates fewer significant system failures. Given the non-linear relationship between the loss function and shortage levels, decreasing the severity of shortages will lead to cost savings. Shih and Revelle [7] presented the discrete hedging technique which is still one of the most practical methods for reservoir management. In this method, shown in Figure 1, when the sum of storage and inflow for a particular month p exceeds V1P, all the demands are fulfilled. If the total storage and inflow are below V1P but above V2P, only 𝜶1 percent of the demand is met, known as the first hedging phase. Similarly, if the total storage and inflow are below V2P but above V3P, 𝜶2 percent of the demand is supplied, termed the second hedging phase [31].

Figure 1: Disceret hedging policy for reservoir operation.

Genetic Algorithm (GA)

Genetic algorithms are stochastic search methods rooted in natural selection and genetics. They commence with an initial array of random solutions known as the initial population. Each entity within this population is termed a chromosome, embodying a potential solution to the problem at hand. Chromosomes progress through successive iterations, referred to as generations. During each iteration, chromosomes undergo evaluation. New generations are generated by either merging two chromosomes from the current generation using a combination operator to create offspring, or by altering a chromosome using a mutation operator to produce the next generation's offspring. Offspring from the current generation become the parents of the subsequent generation. Parent selection for the next generation is facilitated by a selection operator that leverages parental fitness values as a criterion for selection. Weaker chromosomes are then eliminated to maintain a constant population size, ensuring the parents of the next generation are retained. Favorable chromosomes have a greater likelihood of selection, leading the algorithms to converge towards superior chromosomes over several generations, potentially representing the optimal or suboptimal solution [32].

Harmony search algorithm

Harmony Search is an optimization algorithm that simulates the improvisation process of jazz music. In this algorithm, each solution is called a “harmony”. The ‘‘Harmony Memory’’ (HM) matrix is filled with randomly generated solution vectors and sorted in terms of the objective function value. Then, a New Harmony vector is produced based on three parameters: HMCR (harmony memory consideration rate), PAR (pitch adjustment rate), and BW (bandwidth). A good set of parameters can enhance the algorithm’s ability to search for the global optimum. The following general steps are taken in using the HS algorithms. First of all, if a uniform random number returned by rand () (between 0 and 1) is less than HMCR, the decision variable is generated by the memory consideration; otherwise, it is obtained by a random selection between Lower Band (LB) and Upper Band (UB). Secondly, each decision variable updated by the memory consideration undergoes a pitch adjustment with a probability of PAR. Thus, every component obtained by the memory consideration is examined to determine whether it should be pitch-adjusted. This operation uses the PAR parameter. In the memory consideration, New Harmony is chosen from harmony memory. And finally, New Harmony is produced by random selection. If the objective function of the New Harmony vector is better than the worst harmony in the HM, the New Harmony is included in the HM, and the existing worst harmony is excluded from the HM. Then, the harmony memory is sorted again. This process is continued until the stopping criterion is obtained [33].

Mahdavi, et al. (2007) modified the original HS to introduce an improved HS (IHS) algorithm, which dynamically updates the values of PAR and BW as follows [27]:

$PAR(gn)=PAR(\min )+\frac{PAR(\max )-PAR(\min )}{NI}*gn\text{ (1)}$

$b_w(gn)=b_{w,\max }*\exp (C.gn)\text{ (2)}$

$C=\frac{\ln (\frac{b_{w,\min }}{b_{w,\max }})}{NI}\text{ (3)}$

Where NI is the number of iterations considered to stop the algorithm and gn is the repetition number.

In a nutshell, the new scheme to improvise a new harmony, Xnew, can be summarized as follows:

For (i=1 to n)

If (random_1

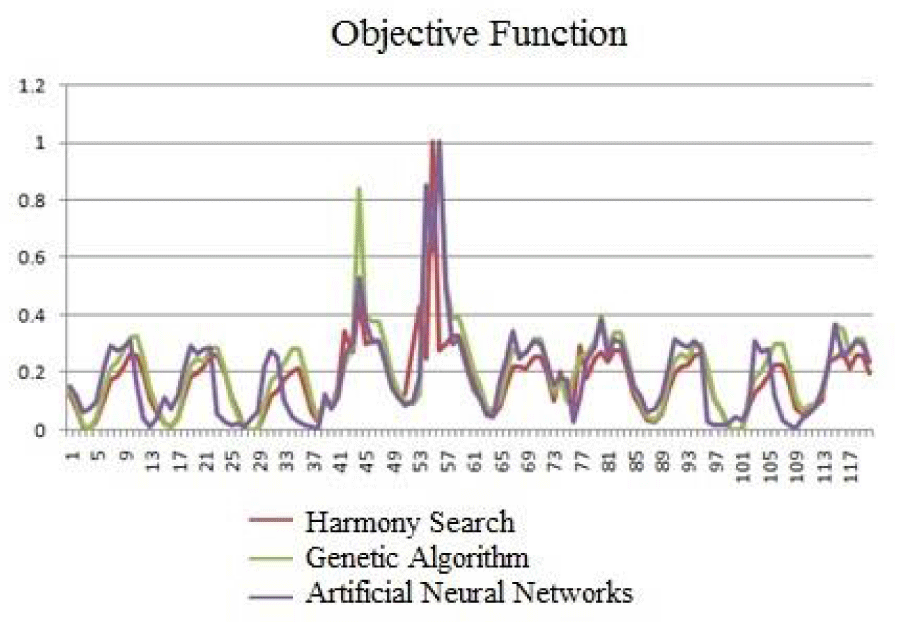
$x\_ne{w}_i=x_i^j$ j ⋳ (1, HMS)

if (random_2

x_newi = x_newi ± random_3 * bw, random_3⋳(0,1)

End if

Else

x_newi = LB(i) + random_4 * (UB(i)-LB(i)), random_4⋳(0,1)

End if

End for

In this algorithm, it is assumed that the HMCR (between 0.9 and 1) and PAR (between 0 and 1) values are normally distributed with a mean of 0.98 and 0.3 and a standard deviation of 0.01 and 0.05, respectively. During the evolution, the values of HMCR and PAR associated with the generated harmony successfully replacing the worst member in the HM are recorded. After a specified number of generations of LP, the means are recalculated by averaging all the recorded values during this period. With the new mean and the given standard deviation, new HMCR, and PAR values are produced and used in the subsequent iterations. The above procedure is repeated.

Case study

Dez is the tallest double-arched concrete dam in Iran, constructed on the main branch of the Dez River. The river flows approximately 420 kilometers before reaching Reservoir Lake, where it merges with the Karun River, eventually emptying into the Persian Gulf. This multipurpose reservoir serves various functions, including providing water for agricultural purposes in fertile plains spanning around 125,000 hectares, generating 520 megawatts of electricity, mitigating river floods and associated damages, and supplying water for industrial needs. The watershed area covers 17,430 square kilometers, with the lake holding a total volume of 3,460 million cubic meters at a height of 352 meters, including 65 million cubic meters of dead storage.

The statistical period spans 42 years, as shown in Table 1. To facilitate method examination and create critical system conditions, the total demand across all periods is assumed to be double the actual value.

Results and discussion

The neural network model for the Dez reservoir in this study comprises three layers: input, hidden, and output. The input layer incorporates inflow, demand, and two seasonality indexes. Given the consistent pattern of inflow data and reservoir output each month, the seasonality indexes are an important input in seasonal models. These indexes help the network to distinguish among different periods within a year. Without seasonality indexes, one must develop a separate model for each seasonal step (month in here) and face up using several models at a time, which would not be an efficient way to handle the problem [34]. We tested several types of seasonality indexes and found the one suggested by Nilsson, et al. [35] to be more suitable for our model. In this method two time series are considered as input neurons which combined, are representative of the cyclic 12 months of the year. One series is represented by the oscillation of a sine curve and the other of a cosine curve. The whole annual cycle is represented by 12 cyclic pairs of values, one unique pair per each month.

The hidden layer houses 2 internal neurons utilizing the sigmoid transfer function. The number of neurons in the hidden layer is obtained by sensitivity analysis through a trial and error process.

The output layer features a single neuron determining the reservoir outflow, employing the linear transfer function. Training the network involves the harmony search algorithm to minimize the total deficiency objective function. The network's weights serve as decision variables for the harmony search algorithm, initially set randomly. Upon each program execution, the harmony search algorithm optimizes the weights to minimize the total deficits' sum.

Moreover, the combination of a neural network and discrete hedging model is utilized for optimal resource operation. In this model, alpha coefficients were set to 0.75 and 0.6 with sensitivity analysis. The neural network comprises three layers: input, hidden, and output. The input layer includes inflow, initial storage, previous period's outflow, demands, alpha coefficients, and two neurons for seasonality indexes. The hidden layer houses 5 internal neurons using the sigmoid transfer function. The output layer features one neuron employing the linear transfer function to determine the reservoir outflow. In this model, based on water availability, one of the neurons 1𝜶, 2𝜶, or 3𝜶 is fed into the system, and network coefficients are adjusted accordingly.

For comparing different methods, various factors have been examined, such as reliability, maximum vulnerability, resiliency, quantitative reliability, deficiency value, and objective function value. The objective function values are shown in Figure 2. It is evident that these values are quite similar and exhibit a consistent trend.

Figure 2: Comparison of objective function values in the studied models.

The evaluation criteria are presented in Table 2. It is important to note that these results reflect an average of 10 executions. It is evident that the neural network method exhibits higher reliability compared to the genetic algorithm and harmony search. Reliability, defined as the proportion of fully covered courses to the total number of courses [27], is notably high in the neural network, the combination of neural network and hedging, and the genetic algorithm, followed by the harmony search algorithm. The maximum annual vulnerability represents the most severe deficiency experienced throughout the simulation period. A lower value indicates a reduced occurrence of significant system failures. Vulnerability is determined by equation (4), where TDt represents the monthly demand and Rt signifies the allocated water amount in month t.

As can be seen, the first three models have a similar maximum vulnerability value but with the combination of the discrete hedging policy and the neural network, this value is significantly reduced to 0.84. This is completely consistent with the philosophy of hedging, which is to increase the number of failures and reduce the maximum shortage. The purpose of hedging in the reservoir operation is to reduce the maximum vulnerability and as a result, reduce the damage caused by a severe shortage. Given the non-linear relationship between the loss function and shortage levels, decreasing the severity of shortages will lead to cost savings. The change in vulnerability is similar to the change in reliability, meaning that increasing reliability causes an increase in vulnerability and vice versa. High values of reliability and low vulnerability are desirable, which is in contradiction with the trend of changes in these two evaluation criteria. However, as can be seen, the vulnerability value is significantly reduced in the last model with a slight decrease in reliability. This is a very important achievement in reservoir operation rule curves.

Conclusion

This study focused on optimizing Dez reservoir operation over a long-term period using a nonlinear loss function through an evolutionary artificial neural network algorithm. The outcomes of this approach were then contrasted with genetic exploration and harmony search algorithms, highlighting the strengths and weaknesses of each method. Ultimately, a combination of the evolutionary artificial neural network method and hedging policies was employed for optimal reservoir management, with results compared to the previous approach. Results showed the appropriate performance of combining hedging policy with artificial neural network and harmony search algorithm. This combination significantly reduced the vulnerability value with a slight decrease in reliability.

1. Bower BT, Hufschmidt MM, Reedy WW. Operating procedures: Their role in the design of water-resources systems by simulation analyses”, in Design of Water Resources Systems, Maass, et al. (eds), Harvard University Press, Cambridge, M.A. 1962; 443-458.
2. Klemes V. Value of information in reservoir optimization. Water Resources Research. 1977; 13(5): 857–850.
3. Stedinger JR. Comment on value of information in reservoir optimization. Water Resource. Research. 1978; 14(5): 984–986.
4. Loucks DP, Stedinger JR, Haith DA. Water resources systems planning and analysis. Prentice-Hall, Englewood Cliffs, NJ. 1981.
5. Hashimoto T, Stedinger JR, Loucks DP. Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation, Water Resources Research. 1982; 16(1): 14-20.
6. Bayazit M, Unal E. Effects of hedging on reservoir performance. Water Resources Research. 1990; 26(4): 713–719.
7. Shih JS, Revelle C. Water supply operation during drought: continuous hedging rule. ASCE, Journal of Water Resources Planning and Management. 1994; 120(5): 613–629.
8. Shih JS, Revelle C. Water supply operation during drought: A discrete hedging rule. European Journal of Operational Research. 1995; 82: 163-175.
9. Hagan MT, Dcmuth HB, Beale M. Neural network design, PWS publishing company. 1996.
10. Chiang YM, Chang LC, Chang FJ. Comparison of static-feed forward and dynamic-feedback neural networks for rainfall–runoff modeling, Journal of Hydrology. 2004; 290(3-4): 297-311.
11. Kumar K, Singh V, Roshni T. Application of the PSO–neural network in rainfall–runoff modeling. Water Practice & Technology. 2023; 18(1): 16-26.
12. Ehteram M, Ahmed AN, Sheikh Khozani Z, El-Shafie A. Convolutional neural network-support vector machine model-gaussian process regression: a new machine model for predicting monthly and daily rainfall. Water Resources Management. 2023; 37(9): 3631-3655.
13. Bai T, Tahmasebi P. Graph neural network for groundwater level forecasting. Journal of Hydrology. 2023; 616: 128792.
14. Sasikala S, Bharatula SD. IoT-Based Smart Irrigation System Based Adaptive Radial Deep Neural Network (ARDNN) Algorithm Applicable for Various Agricultural Production. International Journal of Intelligent Systems and Applications in Engineering. 2024; 12(13s): 351-366.
15. Kangrang A, Prasanchum H, Sriworamas K, Ashrafi SM, Hormwichian R, Techarungruengsakul R, Ngamsert R. Application of optimization techniques for searching optimal reservoir rule curves: A Review. Water. 2023; 15(9): 1669.
16. Ahmadianfar I, Samadi-Koucheksaraee A, Razavi S. Design of optimal operating rule curves for hydropower multi-reservoir systems by an influential optimization method. Renewable Energy. 2023; 211: 508-521.
17. Chandramouli V, Raman H. Multireservoir modeling with dynamic programming and neural networks, Journal of Water Resources Planning and Management. 2001; 127(2): 89-98.
18. Chang YT, Chang LC, Chang FJ. Intelligent control for modeling of real-time reservoir operation, part II: artificial neural network with operating rule curves, Hydrol Process. 2005; 19(7):1431-44.
19. Chaves P, Chang FJ. Intelligent reservoir operation system based on evolving artificial neural networks. Advances in Water Resources. 2008; 31:926-936.
20. Pianosi F, Thi XO, Soncini-Sessa R. Artificial neural networks and multi objective genetic algorithms for water resources management: an application to the Hoabinh reservoir in Vietnam, Proceedings of the 18th IFAC World Congress, Milano (Italy), August 28 – September 2, 2011.
21. Holland JH. Adaptation in Natural and Artificial Systems, Ann Arbor, University of Michigan Press. 1975.
22. Esat V, Hall MJ. Water resources system optimization using genetic algorithms, Hydroinformatics ’94: Proc. 1st Int. Conf. on Hydroinformatics, Balkema, Rotterdam, The Netherlands. 1994; 225-231.
23. Oliveira R, Louks DP. Operating Rules for Multi-reservoir systems, water resources research. 1997; 33: 839-852.
24. Wardlaw R, Sharif M. Evaluation of genetic algorithms for optimal reservoir system operation. Journal of Water Resources Planning. 1999; 125(1): 25-33.
25. Sharif M, Wardlaw R. Multireservoir systems optimization using genetic algorithms: Case study. J Comput Civ Eng. 2000; 14(4); 255-263.
26. Nicklow J, Reed P, Savic D, Dessalegne T. State of the Art for Genetic Algorithms and Beyond in Water Resources Planning and Management, Journal of Water Resources Planning. 2010. DOI: 10.1061/(ASCE)WR.1943-5452.0000053
27. Geem ZW, Kim JH, Loganthan GV. A New Heuristic Optimization Algorithm: Harmony Search, Society for Modeling and Simulation International (SCS). 2001; 76:2:60-68
28. Mahdavi M, Fesanghary M, Damangir E. An improved harmony search algorithm for solving optimization problems. Applied Mathematics and Computation. 2007; 188:1567–1579
29. Omran GH, Mahdav M. Global-best Harmony Search, Applied Mathematics and Computation. 2008; 198:643–656.
30. Pan QK, Suganthan PN, Tasgetiren MF. A Harmony Search with Ensemble of Parameter Sets, evolutionary computation. 2009; 1815-1820.
31. Pan QK, Suganthan PN, Tasgetiren MF, Liang JJ. A Self-Adaptive Global Best Harmony Search Algorithm for Continuous Optimization Problems. Applied Mathematics and Computation. 2010; 216(3): 830-848.
32. Dariane AB, Karami F. Deriving hedging rules of multi-reservoir system by online evolving neural networks. Water resources management. 2014; 28: 3651-3665.
33. Karami F, Dariane AB. A review and evaluation of multi and many-objective optimization: Methods and algorithms. Global Journal of Ecology. 2022; 7(2): 104-119.
34. Karami F, Dariane AB. Many-objective multi-scenario algorithm for optimal reservoir operation under future uncertainties. Water Resources Management. 2018; 32: 3887-3902.
35. Karami F, Dariane AB. Optimizing signal decomposition techniques in artificial neural network-based rainfall-runoff model. International Journal of River Basin Management. 2017; 15(1): 1-8.
36. Nilsson P, Uvo CB, Berndtsson R. Monthly runoff simulation: Comparing and combining conceptual and neural network models. Journal of Hydrology. 2006; 321: 344-363.