Global Journal of Ecology
A review and evaluation of multi and many-objective optimization: Methods and algorithms
Farzane Karami1* and Alireza B Dariane2
2Department of Civil Engineering, KN Toosi University of Technology, Tehran, Iran
Cite this as
Karami F, Dariane AB (2022) A review and evaluation of multi and many-objective optimization: Methods and algorithms. Glob J Ecol 7(2): 104-119. DOI: 10.17352/gje.000070Copyright
© 2022 Karami F, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.Most optimization problems naturally have several objectives, usually in conflict with each other. The problems with two or three objective functions are referred to as Multi-Objective Problems (MOP). However, many real-world applications often involve four or more objectives, which are commonly recognized as many-objective optimization problems (MaOP). Multi and many-objective algorithms have a great application in engineering science. This study addresses a complete and updated review of the literature for multi and many-objective problems and discusses 32 more important algorithms in detail. Afterward, the ZDT and DLTZ benchmark problems for multi-objective test problems are reviewed. All methods have been studied under recent state-of-the-art quality measures. Moreover, we discuss the historical roots of multi-objective optimization, the motivation to use evolutionary algorithms, and the most popular techniques currently in use.
Introduction
Optimization has been expanding in all areas of engineering, medicine, and the sciences [1]. Most optimization problems naturally have several objectives to be achieved which are usually in conflict with each other. This means that there is no single solution for these problems [2]. One way to handle these types of problems is by using the Pareto front. The Pareto front is the plot of the objective functions whose non-dominated solutions, in the sense that there are no solutions superior in all objectives, are in the Pareto optimal set [3,4]. Mathematically, the problem can be written as follows [5]:
Maximize [f1(x), f2(x), …, fm(x)]
ST: gi(x) ≤ 0, i=1, …, k
There are many methods to handle multiple objective problems. Historically, classical optimization methods suggest converting a multi-objective problem to a single-objective problem by different techniques [6,7]. In these cases, the obtained solution is highly sensitive to the weight vector and user knowledge. Later, evolutionary algorithms were introduced and successfully applied in solving multi-objective problems [8].
Problems with a small number of objectives, mainly in two or three objectives are referred to as Multi-Objective Problems (MOP). However, many real-world applications often involve four or more objectives, which are commonly called as Many-Objective Optimization Problems (MaOP). In many-objective optimization problems, the proportion of non-dominated objective solutions increases rapidly with the number of objectives [9-11]. This leads the Pareto optimality to significantly diminishing selection pressure during the evolutionary process [12-14] which will be explained in more detail later.
There are many techniques for handling multi and many-objective optimization problems. We will use the following classification of optimization approaches in this paper:
1. Multi-objective optimization techniques
a. Mathematical techniques
b. Non-Pareto techniques
c. Pareto techniques
2. Many-objective optimization techniques
3. Ancillary techniques.
There are few surveys on multi and many-objective algorithms. Marler and Arora [15] focused on non-Pareto techniques. Zhou, et al. [16] studied multi-objective problems up to 2011; hence many recent algorithms on multi and many objectives are missing in their review. Also, Giagkiozis, et al. [17], just presented population-based algorithms for multi-objective optimization. Qu, et al. [18], studied the research only related to multi-objective problems. On the other hand, Li, et al. [19], discussed only many-objective algorithms in their study. Their review is based on the category of many-objective algorithms rather than discussing algorithms in detail. In addition, more recent important Ancillary methods are missing in their study. Petchrompo, et al. [20], stated that it is difficult for decision-makers to identify the most promising solutions from the Pareto front. They proposed alternative approaches that can autonomously draw up a shortlist of Pareto optimal solutions so that the results are more comprehensible to the decision-maker. They called these alternative approaches the pruning method.
This study contains a complete and updated review of the literature for both multi and many-objective problems where 32 more important algorithms are discussed in detail. Mathematical methods, Non-Pareto Techniques, Pareto evolutionary techniques for multi-objective problems, many-objective approaches, and ancillary methods which can be added to different algorithms in order to improve their performance are discussed together. Moreover, the benchmarks for multi-objective test problems are reviewed. These make the current study a complete package for multi and many-objective algorithms. All methods have been studied under recent state-of-the-art quality measures. We will discuss the historical roots of multi-objective optimization, the motivation to use evolutionary algorithms, and the most popular techniques currently in use. The rest of this work is organized as follows: sections 2 and 3 introduce multi and many-objective optimization techniques respectively. Section 4 presents ancillary methods which can be added to different algorithms in order to improve their performance. In the last section, we review benchmarks for multi-objective test problems [21-24].
The classifications of multi-objective, many-objective and ancillary optimization approaches are shown in Table 1.
Multi-objective optimization techniques
As it was mentioned earlier, problems with a small number of objectives, mainly two or three objectives are referred to as multi-objective problems (MOP). Methods examined in this section are classified into mathematical, non-Pareto and Pareto techniques.
Mathematical methods: Dynamic Programming (DP) and Stochastic Dynamic Programming (SDP) methods are powerful optimization techniques that solve a multi-stage problem by sequentially optimizing a recursive equation, one stage at a time. At each stage, an optimal value will be assigned to the decision variable depending on the state of the system. While in the deterministic case this decision is based on known information; in the stochastic problem, the decision is based on the probability distribution of the variable [25]. Multi-Objective Dynamic Programming (MODP) and Multi-Objective Stochastic Dynamic Programming (MOSDP) are developed based on the single-objective methods and have been used as techniques for solving problems that involve sequential or multistage decision-making [26-28]. In these methods, one objective is considered the primary objective, and others are assumed as the secondary objectives. Unlike the single-objective DP and SDP, the multi-objective methods use two types of state variables. The first type, also called the primary state variable, represents the primary objective function. The secondary objectives of the system are represented by the second kind of state variables. Here, for particular combinations of secondary state variables, the primary objective is optimized [29]. In these approaches, the levels of secondary state variables are not varied stage-wise [30]. Another approach for MODP and MOSDP is by using weighted aggregation of objective functions [31].
Discretization of the state variables in DP-based methods is a basic limiting factor that affects the performance of the optimization process. Recently, the application of dynamic programming in conjunction with fuzzy sets (FDP) has been suggested as a solution to help in overcoming this problem [29]. Another difficulty in using the DP-based methods is the high computational costs due to the curse of dimensionality.
Non-pareto techniques: Non-Pareto techniques convert the multi-objective problem into a single objective via various methods. Although these techniques are efficient and easy to implement, they are incapable of producing certain portions of the Pareto front. In the following, different non-Pareto techniques are discussed.
Weighted aggregation method: Multiple objective functions are combined into one overall objective function by using weighted aggregation of objective functions depending on the importance of objectives [32-34]. This process is the simplest optimization algorithm, but the solution largely depends on the assumed weights [35-36]. The approximation of the Pareto front becomes more accurate by using a different set of weights. However, many combinations of weights may lead to the same Pareto solution, resulting in a wastage of computational time [37-38]. Moreover, the weighting method cannot identify concavities in the Pareto set [39,40].
Max, where M is the number of objectives [41]
Subject to: gi(x) ≤ 0, i=1, …, k
wj ≥ 0, j=1, …, m
ε-Constraint method: In the constrained method, all objectives except one (the most preferred or primary) are incorporated into the constraint set and the remaining objective is then optimized. The values of the constraints are incremented, and the model is repeated until the Pareto front is sufficiently represented [42-47]. Recently, the application of this method in conjunction with the fuzzy sets has been suggested [48,49].
Goal Programming (GP): In goal programming, all the objectives are incorporated into the constraint set and the aggregation of the differences between the solution and the goals (targets), that we wish to achieve for, is assumed as the objective function to be minimized. The weighted GP approach uses weighted aggregation of the differences [42,50].
Several variants of goal programming such as preemptive GP [51], min-max GP [52], fuzzy GP [53-55], chance-constrained GP [56,57], stochastic GP [58], fractional GP [59] and interval GP [60] have been invented. Ignizio [61] examined goal programming algorithms, their history and methods of solution.
Lexicographic ordering: In the lexicographic ordering method, the user is asked to incorporate priorities of the objectives in order of importance. The model starts with the most important one and proceeds according to the assigned order of the objectives. After optimizing each objective function, this function is turned into a constraint for the subsequent levels of optimization [62-65]. This method is inappropriate when there is a large number of objectives and its performance is affected by the pre-defined ranking of objectives. Recently, the application of this method in conjunction with the fuzzy sets has been suggested [66,67].
VEGA (Vector Evaluated Genetic Algorithm): Schaffer [68] proposed this approach according to the simple genetic algorithm (GA). The difference between GA and VEGA is in the selection operator [69,70]. The method generates a number of subpopulations at each generation by performing proportional selection according to each objective function in turn. In other words, an initial population of size M is divided into k subpopulations (each of size M/k) where K is the number of objective functions [71,72]. The method then applies crossover and mutation operators to the merged subpopulations. The solutions generated by this algorithm are not necessarily globally non-dominated because VEGA selects individuals who excel in one objective, without looking at the others [73,74]. Moreover, merging subpopulations is similar to the aggregating techniques, so this algorithm has the drawbacks of the weighting method too.
Pareto techniques: Pareto front-based methods use non-domination ranking and selection to move the population toward the final solution. In other words, solutions in a population are ranked based on the fronts they belong to. As it was mentioned earlier, the Pareto front is the plot of the objective functions whose non-dominated solutions, in the sense that there are no solutions superior in all objectives, are in the Pareto optimal set. Moreover, these methods need a special operator such as fitness sharing, crowding distance, and Cell-based density techniques to maintain the diversity in the population. The solution with a lesser domination rank is preferred when two solutions lie on different fronts. But when both belong to the same front, the one in a less dense region is preferred. Fitness sharing encourages search in unexplored regions and causes subpopulations to form by using penalties for individuals in crowded regions (Figure 1). The fitness sharing operator is calculated by the following equations [75]:
Where, x and y are individuals, zmax and zmin are maximum and minimum of objective functions, K is the number of objective functions and σshare is the sharing radius. A drawback of fitness sharing is the difficulty in estimating the sharing radius beforehand. The other is that the radius in the fitness-sharing method is supposed to be the same for all stages throughout the problem.
The crowded distance of a solution is defined as the average distance of its two neighboring solutions along each objective axis (Figure 2). Solutions with higher crowding distances are preferred due to more spreading. The operator is calculated by the following equations [75].
Cell-based density operator divides the original objective space into cells and the density value of a cell is defined as the number of individuals located in it. Solutions with lower density are preferred. This operator is demonstrated in 10.17352/gje.000070 3.
In the following subsections, different Pareto techniques are discussed.
NSGA, NSGA-II (Non-dominated Sorting Genetic Algorithm): Genetic algorithm [76] has been a popular evolutionary method for solving single as well as multi-objective optimization problems [77]. The non-dominated sorting genetic algorithm (NSGA) proposed by Srinivas and Deb [78], is one of the first evolutionary-based multi-objective algorithms. The main criticisms of the NSGA approach are the high computational complexity of non-dominated sorting, lack of elitism, and specifying the sharing parameter (σshare). Deb, et al. [79], addressed these issues and proposed NSGA-II as an improved version of NSGA. This algorithm has been successfully applied to various multi-objective optimization problems [10,80-88].
The NSGA-II starts with a random generation of a parent population. The initial population members are ranked on the basis of their non-dominated level and crowding distance. Next, through tournament selection, crossover, and mutation, an offspring population of equal size to the parent population is created. Then, parent and offspring populations are combined together to maintain elitism in successive generations. Members in the combined population are ranked again based on their domination and diversity. Finally, the top half best parameter sets are transferred to the next generation. This procedure is repeated till termination criteria are met [37,40,89-92]. The algorithm is sensitive to the value of the sharing factor which is also its main weakness. Figure 4 shows the flowchart of the NSGA-II algorithm.
NPGA (Niched-Pareto Genetic Algorithm): Horn, et al. [93],
extended the genetic algorithm by using Pareto domination ranking and fitness sharing (i.e., niching). In this algorithm, selection pressure is induced by Pareto ranking and tournament competitions, and diversity is maintained by fitness sharing [94]. Population and tournament sizes, niche radius, crossover and mutation rates are the parameters that control the performance of the algorithm. Figure 5 summarizes the processes of NPGA. The advantage of this algorithm is that the Pareto ranking does not apply to the whole population but it has the disadvantage that the tournament size is also required in addition to the fitness sharing parameter.
MMGA (Macro-Evolutionary Multi-Objective Genetic Algorithm): Chen, et al. [95], developed an efficient macro-evolutionary multi-objective genetic algorithm (MMGA) which allows the macro-evolutionary algorithm (MA) to deal with multi-objective optimization problems due to the capability of diversity preservation. This algorithm replaces the selection operator with macro-evolutionary which uses a connectivity matrix W to dynamically compare the fitness values and similarities of all the strings in one generation. Each item in matrix W, Wi,j(t), measures the influence of individual j on individual i at generation t as [96]:
Where f(i) is the objective value of individual i, and dis(i,j) is the Euclidean distance between i and jth individual. Then, coefficient h is determined for individual i using Equ.7 where t is the generation number. The selection operator (S) determines the individuals which are survived [96].
Accordingly, individuals with positive h (S=1) survived, and the others are eliminated. Vacant sites that are freed by extinct individuals (S=0) are filled by applying two rules. First, if a uniform random number in [0,1] is less than a probability τ, a vacant site Pi(t+1) is filled by generating a new solution randomly, Pnew. Otherwise, the extinct solution, Pi(t) will be influenced by one of the surviving solutions, Pb, to generate a new solution Pi(t+1) [96].
Where τ and ρ are given constants, and λ and ζ are uniformly distributed random numbers in [-1,1] and [0,1] respectively. Chen, et al. [95], showed that MMGA requires low computational time and yields a better spread of solutions than NSGA-II. Hence, it is a suitable approach for complex problems where the computational cost is important. But in return, more parameters are required.
RPSGA (Reduced Pareto Set Genetic Algorithm): The reduced Pareto set genetic algorithm (RPSGA) was proposed by Cunha [97]. Later, in order to overcome some limitations of this algorithm such as the fitness deterioration along the generations and the significant number of parameters, the reduced Pareto set genetic algorithm with elitism (RPSGAe) was developed by Cunha and Covas [98]. This algorithm uses a clustering method for obtaining the ranking function and assigning the fitness values which reduces the number of parameters. But in return, it has a more complex structure than previous algorithms (for more information see Cunha and Covas [98]).
MOCOM-UA (Multi-Objective Complex Evolution): The MOCOM-UA algorithm was proposed by Yapo, et al. [99], in the first step, all the individuals are ranked based on their domination. It is obvious that points with a smaller Pareto ranking should have more chances to be selected. Thus Equation 10 developed accordingly is used to calculate the selection probability, Pi; where s is the population size, ri is the individual rank and Rmax is the largest rank in the population [99].
Once all individuals have been ranked, the set of points with the largest rank (Rmax), is called A. Then, n subsets are constructed where, n is the number of points in set A. each subset (Sj) has n+1 members, one is selected from A without replacement and the remaining n are chosen randomly. This process is repeated for all individuals in the A (j=1, …, n). The worst individual in each subset {Sj} is evolved and improved independently using Equation 11. The new solution replaces the point with the worst rank in each subset and each subset is improved independently [100,101].
Where Snew is the new point, Sw is the point with the worst rank and Sg is the centroid of the subset after excluding Sw. In this algorithm,y=2 and y=0.5 and two new solutions are constructed foe each subset. A dominance test is performed among the Snew and other points in the complex and the worst point are replaced by the selected non-dominatedSnew. This process is continued till Rmax=1 is reached which means all the points have become non-dominated.
Since each subset improves independently, this method is suitable for parallel processing. It should be also noted that the MOCOM-UA algorithm can provide an appropriate Pareto front in the context of hydrologic modeling but other applications of this algorithm have not been examined. Moreover, it has a tendency to converge prematurely for problems with a large number of parameters [102].
MOPSO (Multi-Objective Particle Swarm Optimization): The multi-objective particle swarm optimization algorithm developed by Moore and Chapman [103] combines the Pareto dominance principles and particle swarm optimization (PSO) algorithm. PSO was initially invented by Kennedy and Eberhart [104] through inspiration from the collective behavior of social animals such as bird flocking or fish schooling. In this algorithm, each potential solution is called a particle and the population of solutions is called the swarm [105-107]. The particle Xi(t) at the generation t is updated through the following Equations [108-110]:
Where Vi(t) is velocity, pbesti and gbestt (local and global bests) are the best particles that Xi and the entire swarm have viewed respectively. w is the inertial weight of the particle and controls exploration and exploitation in the search space. r1 and r2 are random numbers in the range [0, 1], and c1 and c2 are specific parameters that control the effect of the personal and global best particles.
Although the MOPSO is a popular algorithm in many fields [16,111-113], premature convergence and easy trapping into regional optimum are the problems. The difficulty in applying a PSO algorithm in multi-objective optimization is that the solution of a problem with multiple objectives is not a single one but a set of non-dominated solutions. Hence, there are no clear concepts of local and global bests [114-116]. There are various types of MOPSOs which use leader particles to guide other particles inside the problem domain [117,118].
Non-dominated sorting PSO uses an external archive for storing leaders set and a non-dominated sorting mechanism. In this approach, the particle has updated its position against all the best positions of the swarm [119]. Sigma-MOPSO assigns the sigma value to each particle and makes the selection pressure higher [120]. Optimized MOPSO uses the crowding distance to filter out leader solutions [106]. Another MOPSO uses the concept of Pareto dominance to determine the flight direction of a particle [121]. Sierra and Coello [122] presented a comprehensive review of the various MOPSOs. Moreover, Gad [123] surveyed all changes that have been made to PSO since its inception in the mid-1990s.
ε- MOEA (ε-Domination Based Multi-Objective Evolutionary Algorithm): The ε-dominance concept allows the algorithm to control the achievable accuracy in the obtained Pareto-optimal solutions [124]. In this method if the difference between solutions is small, they do not dominate each other; thereby good diversity is achieved in a population [125]. The ε-dominance method uses two populations; the main population is initialized randomly and the ε-non-dominated solutions of it are copied to an archive population. Choosing a solution from both populations, the offspring solution is created by crossover. To choose a solution from the main population, the first two individuals are picked up randomly from that population. Next, a domination competition is made and the non-dominated one is chosen. If the two solutions are non-dominated to each other, one of them is selected randomly from the archive population. Solution from ε-non-dominated population is chosen randomly. If the offspring dominates one or more solutions in the main population, it replaces one of them randomly. Otherwise, if any individual dominates the offspring, the offspring is rejected. If neither of the above two cases occur, random replacement is used. Also, the offsprings are compared with each solution of the archive population by ε-dominance test. For this purpose, an array (B) is assigned to each solution in the archive as follows (Equation 14) where M is the number of objectives and f
B= (B1, B2, …, BM)T 14
If array B for the offspring dominates the array of any archive member, it replaces that solution. On the contrary, the offspring is rejected if the array of any solution in the archive population dominates it. If the offspring shares the same B vector with a member in the archive, the usual non-domination check is performed [80].
Despite the mentioned advantages of the algorithm, it should be noted that ε must be defined by the decision maker and a large number of good solutions may be lost if this parameter is not chosen properly. Moreover, extreme individuals and solutions in the horizontal and vertical parts of the Pareto front are lost. Later, Hernandez-Diaz, et al. [128] proposed a modified version of ε-MOEA, called pa ε-dominance, to overcome some limitations of this algorithm.
DE (Differential Evolution): Storn and Price [129] introduced the Differential Evolution algorithm and later elaborated on some of its schemes [130]. The main steps of the DE are initialization, mutation, recombination, and selection [131,132]. It is worthwhile to mention that unlike the similarities of the names, these operators are actually different from those used in EAs [133]. After the initialization of a random population, the mutation operator which plays a key role in the optimization process expands the search space based on the distribution of solutions in the population. For this purpose, two individuals are selected randomly (Xr1,t, Xr2,t) and the weighted difference between them is calculated. The weight is a mutation factor (F). The mutant vectors are created by adding each target vector (Xro,t) to the calculated weighted difference. According to this method, an individual is selected at random for replacement and three different individuals (X) are selected as parents, one of which is set as the main parent. Then, the trial vector (V) is produced as follows [134]:
The trial vector is compared only against its one counterpart target individual and the selection operator chooses the one with better performance. Otherwise, the chosen vector for replacement is retained in the population [135,136]. The process is repeated for several generations until the termination criteria are met.
DE algorithm requires fewer parameters as compared to the other methods which make it suitable for high-dimensional complex problems. Notwithstanding, unstable convergence in the last period and easily being trapped into local optimum are the problems. Gong and Cai [137] presented an improved DE algorithm by combining several features of evolutionary algorithms in a unique manner. Santana-Quintero and Coello [132] and Cai, et al. [138] incorporated the ε-dominance concept into the DE algorithm to solve MOPs.
MOAQ (Multi-objective Ant Colony): This algorithm imitates ants’ behavior, where a family of agents is considered for each objective function. Each family finds solutions that depend on solutions found by the rest of the families [139-141]. The pheromone is updated in each step, in which the corresponding best ant is determined [142-144]. The scheme can be summarized as follows where n and m are considered as the number of families and agents for each family respectively [145]:
i=1
Do j=1, m
Find a solution for objective 1
End do
Do i=2, n
Do j=1, m
Use the solution found with ant j in objective i-1 to constrain the solution for ant j (of objective i)
Find a solution for objective i
End do
End do
Evaluate the found solutions
Do j=1, m
If solution j violets any constraint
Apply punishment to all its components
Else if solution j is non-dominated
Apply reward to all its components
Introduce solution j into the Pareto set
Remove all dominated solutions from the Pareto set
Else (solution j is dominated)
Neither applies punishment nor reward
End if
End do
These steps are repeated until the maximum number of iterations is met or all the solutions are non-dominated. This is an efficient and time-saving algorithm because it searches only a small part of the total search space [146,147]. But the performance of this algorithm depends on the number of objectives and the number of ants. This method is used in many fields [148,149].
Amalgam: The AMALGAM algorithm combines the strengths of multiple meta-heuristics algorithms dynamically [150,151]. Each sub-algorithm generates its share of the offspring creation. The number of offspring that sub-algorithm j must generate during generation t, is calculated as follows where K and are respectively the number of sub-algorithms and offspring that sub-algorithm j contributes to the next generation. The equation has some drawbacks in the inclusion of inferior sub-algorithms, hence other methods for offspring partitioning should be studied. This method takes full advantage of the power of optimization algorithms and performs well with increasing number of dimensions [136].
VEGA+NSGA: Mukta, et al. [72], proposed a new approach by using the ideas behind the NSGA-II and VEGA. In this algorithm, the initial population of size M is subdivided into (k – 1) subpopulations of size M/(k – 1) where k is the number of objective functions (f1 to fk). Subdividing is done with respect to each overlapping pair of objective functions and merging is done through genetic operations. For this purpose, the first subpopulation will be created with respect to the performance of f1 and f2, the second will be created with respect to f2 and f3, and in the same way, the k –1st subpopulation will be created from fk–1 and fk. After ranking all subpopulations, k-2 subpopulations are created from elite members using the NSGA approach. The non-dominated individuals in the two first subpopulations of the current step (non-dominated solutions with respect to f1, f2, and f2, f3 pairs) are used to create the first subpopulation of the next step by applying the crossover operator. In the same way, the last subpopulation of the next step (k-2th,/ subpopulation) is created with respect to fk-2, f
In the VEGA algorithm after shuffling sub-populations, a separate fit value is not calculated but in the combined algorithm more fit values are gradually reached. Also, unlike some other methods such as the NSGA this algorithm is not sensitive to the value of the sharing factor.
SPEA, SPEA2 (Strength Pareto Evolutionary Algorithm): The strength Pareto evolutionary algorithm (SPEA) introduced by Zitzler & Thiele [152] uses a clustering technique to estimate the crowding degree of an individual. SPEA starts with an initial population and an empty archive. At each generation, non-dominated individuals are copied to the archive and for each individual, in this set, a strength value is computed (S(i)). The strength value for individual i in the archive is the number of population members that are dominated by or equal to i divided by the population size plus one. A fitness value F(j) is also assigned to the population members. This fitness of an individual j is calculated by summing the strength values S(i) of all archive members i that dominate or are equal to j plus one. The selection operator is done by means of binary tournaments and the offspring population is generated by recombination and mutation [22,153-155].
The clustering technique used in SPEA may lose outer solutions which should be kept in the archive in order to obtain a good spread of non-dominated solutions. Moreover, this algorithm behaves like a random search algorithm in the case when the archive contains only a single individual because all population members have the same rank regardless of their dominance position. Zitzler, et al. [156] designed SPEA2 to overcome these deficiencies. In SPEA2 each individual i in the archive and the population Pt is assigned a strength value S(i), representing the number of solutions it dominates (Eq. 17). Then, the raw fitness is determined by the strengths of its dominators in both archive and population (Eq. 18). This algorithm considers the kth nearest neighbor of an individual in the population for density estimation [12,156].
Where Pt and are population and archive sets. Also, |.| and ≻ indicate the number of elements in a set and Pareto dominance relation, respectively.
PAES (Pareto Archived Evolution Strategy), PEAS (Pareto Envelope-based Selection Algorithm): Knowles and Corne [157] proposed the local search method named Pareto Archived Evolution Strategy (PAES). Then, Corne, et al. [158] introduced Pareto Envelope-Based Selection Algorithm (PEAS) which incorporates ideas from SPEA and PAES. The PAES divides the entire objective space into a number of hyper-boxes. Each offspring is compared with a continuously updated archive population for its inclusion. If the offspring is non-dominated by the archive population, it is compared with the hyper-box having the maximum number of solutions in it. In the case offspring resides in a less crowded hyper-box, it is accepted and a member from the maximally-crowded hyper-box is deleted at random [80]. In other words, the initial random solution, c, is generated and added to the archive. The solution m is produced by mutating c. If c or any member of the archive dominates m, m is discarded. On the other hand, if m dominates c, c is replaced with m, and m is added to the archive. If neither of the above two cases occurs, a special test is applied to determine which becomes the new current solution and whether to add m to the archive or not. The scheme can be summarized as follows [159]:
If (the archive is not full) then
Add m to the archive
If (m is in a less crowded region of the archive than c) then
Accept m as the new current solution
Else
Maintain c as the current solution
End if
Else
If (m is in a less crowded region than a member in the archive) then
Replace m
If (m is in a less crowded region of the archive than c) then
Accept m as the new current solution
Else
Maintain c as the current solution
End if
Else
If (m is in a less crowded region of the archive than c) then
Accept m as the new current solution
Else
Maintain c as the current solution
End if
End if
End if
The PEAS algorithm is a population-version of PAES which allows more than one member to be present in each hyper-box.
Many-objective optimization techniques
Many-objective optimization has been gaining increasing attention in recent years. As it was mentioned earlier, when the number of objectives exceeds four, the proportion of non-dominated objective solutions increases rapidly. This leads the Pareto optimality to significantly diminishing selection pressure during the evolutionary process [160-162]. Selection pressure reduces reproductive success in a proportion of a population potentially. Visualization of a high-dimensional objective space [163,164] and obtaining a good representation of the Pareto front [84] are also other challenges of many-objective optimization problems. Reducing the number of objectives by keeping the least information about them is the simplest way to deal with these problems [165-168]. However, this approach does not work in many problems; hence, various algorithms have recently been proposed to tackle many-objective problems which are described as follows.
EMaOEA (Ensemble of Many-Objective Evolutionary Algorithms): Zhou, et al. [14] used a combination of Pareto dominance selection, diversity maintenance, and elitism strategy and proposed an ensemble of many-objective evolutionary algorithms (EMaOEA). This algorithm simultaneously runs different many-objective evolutionary algorithms in parallel and maintains interactions between them by merging all offspring subpopulations [169]. Since the performance of MaOEAs may be different from one problem to another, EMaOEA runs them in parallel and maintains interactions between them by a simple information-sharing scheme. Steponavice, et al. [170] used a machine learning technique to switch among different algorithms during the optimization search based on the predicted performance of each algorithm at the time.
HypE (Hypervolume Estimation Algorithm for Multi-Objective Optimization): The hypervolume (HV) indicator [152,171] is a quality indicator that is fully sensitive to Pareto dominance. There have been several well-established hypervolume-based MOEAs available in the literature [172-176]. The main drawback of this indicator is the computational cost of HV which grows exponentially with the number of objectives increasing [177,178]. To address this issue, Bader and Ziztler [179] proposed a fast search algorithm that uses Monte Carlo simulation to approximate the exact hypervolume values. The hypervolume indicator gives the volume of the objective subspace that is dominated by a solution set A ⊂ Rd under consideration. For more details in definitions see Ziztler, et al. [180].
This method is more complicated in comparison with other many-objective algorithms. The main drawback of hypervolume indicator-based algorithms is the high time complexity for measuring the exact hypervolume contributions of different solutions. To cope with this problem, Jiang, et al. [181] proposed Fast hypervolume indicator-based MOEA (FV-MOEA) to quickly update the exact hypervolume contributions of different solutions. In this algorithm, the hypervolume contribution of a solution is only associated with partial solutions rather than the whole solution set for saving time.
GrEA (Grid Based Evolutionary Algorithm): Grid-based algorithms exploit the potential of the grid-based approach to strengthen the selection pressure towards the optimal direction while maintaining an extensive and uniform distribution among solutions. Each solution in the grid has a deterministic location [182]. The number of solutions whose grid locations are analogous reflects diversity. Also, the grid location of an individual compared with other solutions determines the convergence. This approach compares solutions qualitatively and quantitatively [177,178].
The lower (lbk) and upper (ubk) boundaries of the grid for the kth objective with a population P are determined using the following equations, where ndiv is the number of the divisions of the objective space in each dimension [182]:
Hence, the grid width dk in the kth objective can be determined according to the following formula:
Thus, the grid location of a solution in this objective Gk(x) can be calculated by Equation 22 where Fk(x) is the actual objective value in the kth objective:
Yang, et al. [182] take three grid-based criteria into account to assign the fitness of individuals. They are grid ranking (GR), grid coordinate point distance (GCPD), and grid crowding distance (GCD). The convergence of individuals is evaluated by GR and GCPD, while GCD appraises the diversity in the population. By considering M as the number of objectives, these criteria are determined according to the following equations [182]:
N(x) stands for the set of neighbors of x and two individuals x and y are neighbors if GD(x,y)M where,
Note that, the parameter ndiv (the number of divisions) is required to set the grid environment in this algorithm. Also, the effect of the population size has not been investigated in this method.
NSGA-III: Deb and Jain [183] proposed NSGA-III on the basis of the NSGA-II algorithm with significant changes in its selection mechanism for many-objective problems. This algorithm uses a predefined set of reference points H on a unit hyper-plane to ensure diversity in the solutions. The reference points can be predefined in a structured manner or by the user. Ruiz, et al. [184] used the reference points and suggested a preference-based evolutionary multi-objective optimization called weighting achievement scalarizing function genetic algorithm. If M and P are considered as the number of objectives and divisions along each objective respectively, the total number of reference points (H) is given by the following Equation [185]:
In each iteration, an offspring population Qt is created from population Pt, both having size N, using the recombination and mutation operators. Then, the two populations Pt and Qt are merged together to form a new population Rt (of size 2N). Similar to NSGA-II, the best N members from Rt are chosen for the next generation based on Pareto dominance (St). The NSGA-II algorithm selects solutions with the largest crowding distance values which do not perform well on many-objective problems. Hence, NSGA-III uses a pre-defined guidance mechanism to choose diverse solutions for the population. First, the ideal point of the St is determined by identifying the minimum values of each objective function. Then, each objective value of St is normalized by subtracting objective fi by zmin , so that the normalized ideal point of St becomes a zero vector. Afterward, the perpendicular distance between members in St and each of the reference lines (joining the ideal point with a reference point) is computed. All members in St are then affiliated with a reference point having the minimum perpendicular distance. In this way, a reference point may have one, more, or no population members. The number of population members that are associated with the jth reference point is defined as the niche count; ρj. The reference points with a lesser niche count are maintained for the next generation to keep diversity [183]. Studies show that The NSGA-III performs well in different problems and does not depend on the type of the problem. Deb and Jain [183] demonstrated that using reference points and NSGA-III niching methodology makes this algorithm suitable for solving up to 15 objective functions. NSGA-III does not work for less than three objective optimization problems. Seada and Deb [186] developed a unified evolutionary optimization algorithm U-NSGA-III, based on NSGA-III to make it capable of working for bi-objective or mono-objective problems. Yi, et al. [187] introduced an adaptive mutation operator to enhance the performance of the standard NSGA-III algorithm. Zhu, et al. [188] proposed improved NSGA-III by using a novel niche preservation procedure. Gonçalves, et al [189] used adaptive operator selection mechanisms in this algorithm. Tanabe and Oyama [190] investigated the impact of population size, number of children, and number of reference points on the Performance of NSGA-III. It should be noted that the impact of the number of divisions (P) which must be defined by the decision maker is not clear and needs further investigation.
θ-DEA (θ-Dominance Evolutionary Algorithm): NSGA-III relies on Pareto-dominance to push the population towards the Pareto front (PF), leaving room for the improvement of its convergence ability. The θ-dominance evolutionary algorithm, proposed by Yuan, et al. [177], aims to enhance the convergence of NSGA- III by exploiting the fitness evaluation scheme based on decomposition but still inherits the strength of the former in diversity maintenance. The environmental selection mechanism in the proposed algorithm is based on θ-dominance. In θ-DEA, the clustering operator is done to the population St (which was defined in the NSGA-III sub-section) at each generation. The clustering works in the normalized objective space, where the ideal point is the origin. This algorithm enhances the convergence ability of NSGAIII in high-dimensional objective space but θ is the main parameter that must be defined by the decision-maker. For more details see Yuan, et al. [177].
Ancillary methods
The convergence ability of Pareto-based evolutionary algorithms sharply reduces for many-objective optimization problems as the solutions are difficult to rank by the Pareto dominance. In order to help many-objective algorithms to increase the selection pressure toward the global optimal solutions and well-maintain the diversity of the obtained solutions, some ancillary techniques have been proposed in recent years. These ancillary methods which can be merged into the many-objective algorithms are discussed in the following sections.
Fuzzy-based pareto: The concept of fuzzy logic is adopted to define a fuzzy Pareto domination relation in various studies in order to compare two solutions [191-193].
Eshtehardian, et al. [194] embedded fuzzy sets theory into GA to solve the discontinuous and multi-objective fuzzy time-cost model with a fairly large search space. He, et al. [11], applied the fuzzy set based on the left Gaussian function to quantify the degrees of domination, ranging from dominating to being dominated and in between, with various degrees of domination in each objective. The fuzzy approach deals with uncertainties and the fuzzy-based Pareto lets the decision-maker use his own level of risk acceptance. Also, this method addresses the impact of uncertainties related to data. Nevertheless, selecting an appropriate fuzzy function has an important role in this method.
Set-based: In set-based many-objective algorithms, each objective of the original optimization problem is transformed into a desirability function according to the preferred region defined by the decision maker. Afterward, the transformed problem is converted to a bi-objective optimization one by taking hyper-volume and the decision maker’s preferences as the new objectives, and a set of solutions of the basic optimization problem as the new decision variable [195]. If the range of the ith objective function is explained as , the DM’s preferred region in the ith objective is represented as where . Hence, the minimum and maximum objective functions are required in this method. Considering all objectives, the preferred region can be formulated as where M is the number of objectives. Obviously, the DM’s preferred region is a hypercube in the objective space for many-objective problems. Thereafter, the objectives are normalized by the following formula; where di(fi(x)) is the ith normalized objective function [116,195].
By mapping the values αi and βi into the bounds of the normalized objectives, the values of ai and bi are obtained.
Gong, et al. [195] proposed a set-based genetic algorithm and used a genetic algorithm to tackle the converted bi-objective optimization problem. Later, an improved set evolution multi-objective particle swarm optimization (S-MOPSO, for short) was proposed by Sun, et al. [116].
This method dynamically determines a preferred region to guide the algorithm. Although using this ancillary method makes high computational complexity, it can improve the convergence and the distribution of the Pareto front.
GPO (Generalized Pareto Optimality): Aiming at improving the scalability of Pareto-based MOEAs, Zhu, et al. [196] generalized the Pareto optimality, both symmetrically and asymmetrically, by providing nondiscriminatory expansions of the dominance area of solutions. With the aid of the generalized Pareto optimality technique (GPO), many-objective evolutionary algorithms could acquire the flexibility of changing their selection pressure within certain ranges, which would allow them to maintain their evolvability when dealing with problems with many-objectives [196]. Despite the abovementioned advantages, it is worth noting that the method is difficult to understand and implement.
α-Dominance: The α-dominance strategy was proposed by Ikeda, et al. [197] and improved by Dai, et al. [198]. This method increases the selection pressure by modifying the fitness values. It should be noted that if the value of α is too large, the selection pressure will be enhanced, but it may cause some optimal solutions with their objective vectors in the intermediate region of the objective space to become dominated solutions under this dominance strategy. On the other hand, if the value of α is too small, it would be difficult to ensure the convergence of solutions to the true Pareto front. Therefore, assigning a suitable value of α to improve the convergence and maintain the diversity is a very crucial and also difficult for this strategy.
This method permits a solution x to dominate another solution z, if x is slightly inferior to z in one objective while largely superior to z in some other objectives. For this purpose, a relative fitness vector t (x, z) is calculated by the following equation and the dominance relation is determined by this value [198]:
Where fi (x) is the fitness value of solution x on the ith objective.
SDE (Shift-Based Density Estimation): Shift-based density estimation tries to “put” individuals with poor convergence into crowded regions. For this purpose, the poorly converged individuals are assigned a high-density value, which helps them to be eliminated easily during the evolutionary process. In this method, after estimating the density of an individual A, the positions of other individuals in the population are shifted according to the comparison of convergence between these individuals and A on each objective. It means that if an individual performs better than A for an objective, SDE shifts it to the same position as A on this objective. Li, et al [107] provide an example to clarify the issue. They considered a population of four non-dominated individuals A, B, C, and D with their objective value (0, 1, 1, 100), (1, 0, 2, 1), (2, 1, 0, 1), and (1, 2, 1, 0). In this population, individual A performs the worst regarding convergence. This individual also has a higher probability of selection operator than those poorly converged non-dominated individuals. The shift-based density estimation strategy is proposed to end this.
DBEA (Decomposition Based Evolutionary Algorithm): Decomposition is a basic strategy in traditional multi-objective optimization which has been studied to deal with many-objective optimization problems [199]. Jain and Deb [183] used a scaling method to deal with objectives in different orders of magnitude. Asafuddoula, et al. [200] proposed the decomposition-based evolutionary algorithm with epsilon level comparison (DBEA-Eps) relied on using an adaptive epsilon level comparison to avoid aggregation. In this algorithm, a hyperplane was constructed using M extreme non-dominated solutions which in turn provided the lengths of the axis intercepts. DBEA-Eps is further improved (I-DBEA) by the authors [201]. This ancillary method makes high computational complexity but can improve the performance of the algorithm.
Social choice: Dariane and Karami [202] provided a many-objective optimization algorithm using social choice (SC) and melody search (MeS) algorithms. They showed that the proposed many-objective algorithm is able to handle as many objectives as needed without any computational burden and/or algorithm complexity. The social choice (SC) procedures are voting systems for group decision-making when available information is minimal, or mainly qualitative [203]. The subject is to derive social orderings when individual welfare satisfies certain assumptions [204].
Test benchmarks
Benchmark problems are important for evaluating the algorithms. Test problems should be easy to describe, easy to understand and visualize, and easy to implement and their optima are often known in advance [205]. The six test problems called The ZDT Tests, created by Zitzler, et al. [22], are the most widely employed benchmarks for multi-objective problems. A variety of research studies use ZDT problems for evaluating their algorithms which facilitates comparisons with new algorithms. However, the ZDT problems have only two objectives thus they are not suitable for MaOEA.
The DTLZ benchmark problems, created by Deb, et al. [23], represent a considerable step forward, as they allow researchers to investigate the properties of many-objective problems in a controlled manner, with known problem characteristics and knowledge of the Pareto optimal front. The five real-valued ZDT and DTLZ problems are presented in Table 2 [206], noting that ZDT5, the omitted problem, is binary encoded and has often been omitted from the analysis.
Conclusion
In this study, a complete and updated review of the literature for multi and many-objective problems has been surveyed. The historical roots of multi-objective optimization, the motivation to use evolutionary algorithms, and the most popular techniques currently in use were discussed. Moreover, the ZDT and DLTZ benchmark problems for multi-objective test problems were reviewed.
- Butenko S, Pardalos PM. Extended Frontiers in Optimization Techniques. In: New Optimization Techniques in Engineering. Springer Berlin Heidelberg, Berlin, Heidelberg. 2004; 703-712
- Srdjevic B, Medeiros Y, Faria AS. An objective multi-criteria evaluation of water management scenarios. Water Resour Manag. 2004; 18:35-54. doi: 10.1023/B:WARM.0000015348.88832.52
- Minami M. Weak Pareto optimality of multiobjective problems in a locally convex linear topological space. J Optim Theory Appl. 1981; 34:469-484. doi: 10.1007/BF00935888
- Kaliszewski I, Miroforidis J. Two-Sided Pareto Front Approximations. J Optim Theory Appl. 2014; 162:845–855. doi: 10.1007/s10957-013-0498-y
- Konak A, Coit DW, Smith AE. Multi-objective optimization using genetic algorithms: A tutorial. Reliab Eng Syst Saf. 2006; 91:992-1007. doi: 10.1016/j.ress.2005.11.018
- Ashrafi SM, Dariane AB. Unconstrained Numerical Optimization Using Triple Alternative Improvisation Scheme. In: 12th International Conference on Hybrid Intelligent Systems (HIS12). Pune, India. 2012.
- Ashrafi SM, Dariane AB. Performance evaluation of an improved harmony search algorithm for numerical optimization: Melody Search (MS). Eng Appl Artif Intell 26:1301–1321. doi: 10.1016/j.engappai. 2013; 2012.08.005
- Deb K, Sinha A. Solving bilevel multi-objective optimization problems using evolutionary algorithms. Evol Multi-Criterion Optim 5th Int Conf EMO. 2009; 110–124.
- Fleming PJ, Purshouse RC, Lygoe RJ. Many-objective optimization: an engineering design perspective. Lect Notes Comput Sci. 2005; 3410/2005:14–32. doi: 10.1007/978-3-540-31880-4_2
- Adra SF, Fleming PJ. Diversity management in evolutionary many-objective optimization. IEEE Trans Evol Comput. 2011; 15:183–195. doi: 10.1109/TEVC.2010.2058117
- He Z, Yen GG, Zhang J. Fuzzy-based pareto optimality for many-objective evolutionary algorithms. IEEE Trans Evol Comput. 2014; 18:269–285. doi: 10.1109/TEVC.2013.2258025
- Li M, Yang S, Liu X. Shift-based density estimation for pareto-based algorithms in many-objective optimization. IEEE Trans Evol Comput. 2014; 18:348–365. doi: 10.1109/TEVC.2013.2262178
- Ma X, Qi Y, Li L. MOEA/D with uniform decomposition measurement for many-objective problems. Soft Comput. 2014; 18:2541–2564. doi: 10.1007/s00500-014-1234-8
- Zhou Y, Wang J, Chen J. Ensemble of many-objective evolutionary algorithms for many-objective problems. Soft Comput. 2015; doi: 10.1007/s00500-015-1955-3
- Marler RT, Arora JS. Survey of multi-objective optimization methods for engineering. Struct Multidiscip Optim. 2004; 26:369–395. doi: 10.1007/s00158-003-0368-6
- Zhou A, Qu B-Y, Li H. Multiobjective evolutionary algorithms: a survey of the state of the art. Swarm Evol Comput. 2011; 1:32–49. doi: 10.1016/j.swevo.2011.03.001
- Giagkiozis I, Purshouse RC, Fleming PJ. An overview of population-based algorithms for multi-objective optimisation. Int J Syst Sci. 2015; 46:1572–1599.
- Qu BY, Zhu YS, Jiao YC. A survey on multi-objective evolutionary algorithms for the solution of the environmental/economic dispatch problems. Swarm Evol Comput. 2018; 38:1–11. doi: https://doi.org/10.1016/j.swevo.2017.06.002
- Li B, Li J, Tang K, Yao X. Many-objective evolutionary algorithms: A survey. ACM Comput Surv. 2015a; 48:13. doi: 10.1145/2792984
- Petchrompo S, Coit DW, Brintrup A, Wannakrairot A, Parlikad AK. A review of Pareto pruning methods for multi-objective optimization. Computers & Industrial Engineering. 2022;108022
- Deb K. Multi-objective genetic algorithms: problem difficulties and construction of test problems. Evol Comput. 1999 Autumn;7(3):205-30. doi: 10.1162/evco.1999.7.3.205. PMID: 10491463.
- Zitzler E, Deb K, Thiele L. Comparison of multiobjective evolutionary algorithms: empirical results. Evol Comput. 2000 Summer;8(2):173-95. doi: 10.1162/106365600568202. PMID: 10843520.
- Deb K, Thiele L, Laumanns M, Zitzler E. Scalable test problems for evolutionary multiobjective optimization. Evol Multiobjective Optim Theor Adv Appl. 2005b; 105–145. doi: 10.1007/1-84628-137-7_6
- Khan A, Naz BS, Bowling LC. Separating snow, clean and debris covered ice in the Upper Indus Basin, Hindukush-Karakoram-Himalayas, using Landsat images between 1998 and 2002. J Hydrol. 2015; 521:46–64. doi: 10.1016/j.jhydrol.2014.11.048
- Serrat-Capdevila A, Valdes JB. An alternative approach to the operation of multinational reservoir systems: Application to the Amistad and Falcon system (Lower Rio Grande/Rio Bravo). Water Resour Manag. 2007; 21:677–698. doi: 10.1007/s11269-006-9035-1
- Daellenbach H, Kluyver A. Note on multiple objective dynamic programming. J Oper Res Soc. 1980; 31:591–594.
- Saadouli N, Edirisinghe C. Multi-stage stochastic model for a multipurpose water reservoir with target-priority operation. Water. 2006:146–151.
- Dabia S, Woensel T Van, Kok AG De. Time-dependent capacitated single vehicle routing a dynamic programming approach to multi-objective time-dependent capacitated single vehicle routing problems with time windows. 2010.
- Abo-Sinna MA. Multiple objective (Fuzzy) dynamic programming problems: A survey and some applications. Appl Math Comput. 2004; 157:861–888. doi: 10.1016/j.amc.2003.08.083
- Talkudar B, Deb D, DK S. Development of multiobjective stochastic dynamic programming (MOSDP) reservoir operation model. In: World Environmental and Water Resources Congress. 2012; 985–997.
- Villarreal B, Karwan M. Multicriteria integer programming: a hybrid dynamic programming recursive approach. Math Program. 1981; 21:204–223. doi: 10.1007/BF01584241
- Cohon JL, Marks DH. A review and evaluation of multiobjective programming techniques. Water Resour Res. 1975; 11:208–220.
- Liang Q, Johnson L, Yu Y. A comparison of two methods for multi-objective optimization for reservoir operation. , J Am water Resour Assoc. 1996; 32:333–340. doi: 10.13140/2.1.4291.7446
- Agrell PJ, Lence BJ, Stam A. An interactive multicriteria decision model for multipurpose reservoir management the Shellmouth Reservoir. J Multi-Criteria Decis Anal. 1998; 7:61–86. doi: 10.1002/(SICI)1099-1360(199803)7:2<61::AID-MCDA173>3.0.CO;2-L
- Jakob W, Gorges-Schleuter M, Blume C. Application of genetic algorithms to task planning and learning. Parallel Probl Solving from Nature, 2nd Work. 1992; 291–300. doi: 10.1109/ISATP.1999.782993
- Blickle T, Teich J, Thiele L. System-level synthesis using evolutionary algorithms. Des Autom Embed Syst. 1998; 58:23–62. doi: 10.1023/A:1008899229802
- Pianosi F, Thi XQ, Soncini-Sessa R. Artificial neural networks and multi objective genetic algorithms for water resources management: an application to the Hoabinh reservoir in Vietnam. IFAC Proc. 2011; 18:10579–10584. doi: 10.3182/20110828-6-IT-1002.02208
- Schardong A, Simonovic S. Multi-objective evolutionary algorithms for water resources management. 2011.
- Das I, Dennis JE. A closer look at drawbacks of minimizing weighted sums of objectives for Pareto set generation in multicriteria optimization problems. Struct Optim. 1997; 14:63–69. doi: 10.1007/BF01197559
- Reddy MJ, Kumar DN. Optimal reservoir operation using multi-objective evolutionary algorithm. Water Resour Manag. 2006; 20:861–878. doi: 10.1007/s11269-005-9011-1
- Ren J, Ren X, Liang H. Multi-actor multi-criteria sustainability assessment framework for energy and industrial systems in life cycle perspective under uncertainties. Part 1: weighting method. Int J Life Cycle Assess. 2017; 22:1397–1405. doi: 10.1007/s11367-016-1251-1
- Ko S-K, Fontane DG, Labadie JW. Multiobjective optimization of reservoir systems operation. J Am Water Resour Assoc. 1992; 8:111–127. doi: 10.1111/j.1752-1688.1992.tb03158.x
- Schott JR. Fault tolerant design using single and multi-criteria genetic algorithms. Massachusetts Institute of Technology. 1995.
- Lee C-Y. Minimizing the makespan in the two-machine flowshop scheduling problem with an availability constraint. Oper Res Lett. 1997; 20:129–139. doi: 10.1016/S0167-6377(96)00041-7
- Btissam D, Rachida A. Multi-Objective examination Timetabling Problem : Modeling and resolution using a based ε -constraint method. 2017; 17:192–198.
- Chen J, Li J, Xin B. DMOEA-ϵC : Decomposition-based multiobjective evolutionary algorithm with the ϵ -constraint framework. IEEE Trans Evol Comput. 2017; 21:714–730. doi: 10.1109/TEVC.2017.2671462
- Batista AC, Batista LS. Demand Side Management using a multi-criteria ϵ-constraint based exact approach. Expert Syst Appl. 2018; 99:180–192. doi: https://doi.org/10.1016/j.eswa.2018.01.040
- Nojavan S, Majidi M, Najafi-Ghalelou A. A cost-emission model for fuel cell/PV/battery hybrid energy system in the presence of demand response program: ε-constraint method and fuzzy satisfying approach. Energy Convers Manag. 2017; 138:383–392. doi: https://doi.org/10.1016/j.enconman.2017.02.003
- Balaman ŞY, Matopoulos A, Wright DG, Scott J. Integrated optimization of sustainable supply chains and transportation networks for multi technology bio-based production: A decision support system based on fuzzy ε-constraint method. J Clean Prod. 2018; 172:2594–2617. doi: https://doi.org/10.1016/j.jclepro.2017.11.150
- Coello C. Evolutionary multi-objective optimization: a critical review. In: Evolutionary Optimization. 2000c; 117–146.
- Wang YM, Parkan C .A preemptive goal programming method for aggregating OWA operator weights in group decision making. Inf Sci (Ny) .2007; 177:1867–1877. doi: 10.1016/j.ins.2006.07.023
- Loganathan G V, Bhattacharya D .Goal-programming techniques for optimal reservoir operations. J Water Resour Plan Manag . 1990;116:820. doi: 10.1061/(ASCE)0733-9496(1990)116:6(820)
- Sharma DK, Jana RK Fuzzy goal programming based genetic algorithm approach to nutrient management for rice crop planning. Int J Prod Econ 2009;121:224–232. doi: 10.1016/j.ijpe.2009.05.009
- Deliktas D, Ustun O .Student selection and assignment methodology based on fuzzy MULTIMOORA and multichoice goal programming. Int Trans Oper Res 2017; 24:1173–1195. doi: 10.1111/itor.12185
- Trivedi A, Singh A .A hybrid multi-objective decision model for emergency shelter location-relocation projects using fuzzy analytic hierarchy process and goal programming approach. Int J Proj Manag 2017; 35:827–840. doi: https://doi.org/10.1016/j.ijproman.2016.12.004
- Changchit C, Terrell MP .A multiobjective reservoir operation model with stochatic inflows. Comput Ind Eng 1993; 24:303–313. doi: 10.1016/0360-8352(93)90016-Q
- Yang W, Zhao S, Zhou Z. Risk Adjustable Day-Ahead Unit Commitment With Wind Power Based on Chance Constrained Goal Programming. IEEE Trans Sustain Energy 2017; 8:530–541. doi: 10.1109/TSTE.2016.2608841
- Al-Zahrani MA, Ahmad AM .Stochastic goal programming model for optimal blending of desalinated water with groundwater. Water Resour Manag 2004;18:339–352. doi: 10.1023/B:WARM.0000048487.05662.88
- Fasakhodi AA, Nouri SH, Amini M .Water resources sustainability and optimal cropping pattern in farming systems; a multi-objective fractional goal programming aqpproach. Water Resour Manag 2010; 24:4639–4657. doi: 10.1007/s11269-010-9683-z
- Sen S, Pal BB .Interval goal programming approach to multiobjective Fuzzy goal programming problem with interval weights. Procedia Technol 2013;10:587–595. doi: 10.1016/j.protcy.2013.12.399
- Ignizio PJ .A Review of Goal Programming: A Tool for Multiobjective Analysis. J Oper Res Soc 1978; 29:1109–1119. doi: 10.1057/jors.1978.243
- Dauer JP, Krueger RJ . A multiobjective optimization model for water resources planning. Appl Math Model 1980; 4:171–175. doi: 10.1016/0307-904X(80)90127-4
- Gacôgne L .Research of Pareto set by genetic algorithm, application to multicriteria optimization of Fuzzy controller. In: 5th European Congress on Intelligent Techniques and Soft Computing EUFIT’97. France, 1997; 837–845
- Jee KW, McShan DL, Fraass BA. Lexicographic ordering: intuitive multicriteria optimization for IMRT. Phys Med Biol. 2007 Apr 7;52(7):1845-61. doi: 10.1088/0031-9155/52/7/006. Epub 2007 Mar 7. PMID: 17374915.
- Schellenberg S, Li X, Michalewicz Z .Preliminary Study on Solving Coal Processing and Blending Problems Using Lexicographic Ordering. In: Peng W, Alahakoon D, Li X (eds) AI 2017: Advances in Artificial Intelligence. Springer International Publishing, Cham, 2017; 221–233
- Ebrahimnejad A .A lexicographic ordering-based approach for solving fuzzy transportation problems with triangular fuzzy numbers. Int J Manag Decis Mak 2017;16:346–374.
- van Haveren R, Ogryczak W, Verduijn GM, Keijzer M, Heijmen BJM, Breedveld S. Fast and fuzzy multi-objective radiotherapy treatment plan generation for head and neck cancer patients with the lexicographic reference point method (LRPM). Phys Med Biol. 2017 Jun 7;62(11):4318-4332. doi: 10.1088/1361-6560/62/11/4318. Epub 2017 May 5. PMID: 28475495.
- Schaffer JD .Multiple objective optimization with vector evaluated genetic algorithms. In: the 1st international Conference on Genetic Algorithms. 1985; 93–100
- Ritzel BJ, Eheart JW, Ranjithan S. problem potential well site hypothetical contaminant.
- Surry PD, Radcliffe NJ, Boyd ID .A multi-objective approach to constrained optimization of gas supply networks. In: Proceedings of the AISB-95 Workshop on Evolutionary Computing. 1995; 166–180
- Richardson J, Palmer M, Liepins G, Hilliard M .Some guidelines for genetic algorithms with penalty functions. In: Third International Conference on Genetic Algorithms. San Francisco, CA, USA, 1989; 191–197
- Mukta SH, Islam TMR, Hasnayen SM .Multi-objective optimization using genetic algorithm. Int J Emerg Trends Technol Comput Sci 2012; 1:255–260.
- Coello C .An updated survey of GA-based multiobjective optimization techniques. ACM Comput Surv 2000; 32:109–143. doi: 10.1145/358923.358929
- Coello C .Treating constraints as objectives for single-objective evolutionary optimization. Eng Optim 2000; 32:275–308. doi: 10.1080/03052150008941301
- Yu X novel clustering fitness sharing genetic algorithm. In: Lecture Notes in Computer Science. Springer Berlin Heidelberg, 2005; 1072–1079
- Goldberg DE .Genetic algorithms in search, optimization, and machine learning. Boston, MA, USA .1989.
- Long Q, Wu C, Huang T, Wang X .A genetic algorithm for unconstrained multi-objective optimization. Swarm Evol Comput. 2015; 22:1–14. doi: 10.1016/j.swevo.2015.01.002
- Srinivas N, Deb K .Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol Comput 1995;2:221--248. doi: 10.1162/evco.1994.2.3.221
- Deb K, Pratab S, Agarwal S, Meyarivan T .A fast and elitist multiobjective genetic algorithm: NGSA-II. IEEE Trans Evol Comput 2002; 6:182–197. doi: 10.1109/4235.996017
- Deb K, Mohan M, Mishra S. Evaluating the epsilon-domination based multi-objective evolutionary algorithm for a quick computation of Pareto-optimal solutions. Evol Comput. 2005 Winter;13(4):501-25. doi: 10.1162/106365605774666895. PMID: 16297281.
- De Vos NJ, Rientjes THM .Multi-objective performance comparison of an artificial neural network and a conceptual rainfall—runoff model. Hydrol Sci J .2007; 52:397–413. doi: 10.1623/hysj.52.3.397
- Baltar AM, Fontane DG .Use of multiobjective particle swarm optimization in water resources management. J Water Resour Plan Manag 2008; 134:257–265.
- Hakimi-Asiabar M, Ghodsypour SH, Kerachian R .Deriving operating policies for multi-objective reservoir systems: application of self-learning genetic algorithm. Appl Soft Comput J . 2010;10:1151–1163. doi: 10.1016/j.asoc.2009.08.016
- Ishibuchi H, Akedo N, Nojima Y .Behavior of multiobjective evolutionary algorithms on many-objective knapsack problems. IEEE Trans Evol Comput 2015; 19:264–283. doi: 10.1109/TEVC.2014.2315442
- Esfe MH, Razi P, Hajmohammad MH.Optimization, modeling and accurate prediction of thermal conductivity and dynamic viscosity of stabilized ethylene glycol and water mixture Al2O3 nanofluids by NSGA-II using ANN. Int Commun Heat Mass Transf 2017; 82:154–160. doi: https://doi.org/10.1016/j.icheatmasstransfer.2016.08.015
- Vo-Duy T, Duong-Gia D, Ho-Huu V.Multi-objective optimization of laminated composite beam structures using NSGA-II algorithm. Compos Struct 2017; 168:498–509. doi: https://doi.org/10.1016/j.compstruct.2017.02.038
- Esfe MH, Razi P, Hajmohammad MH. Corrigendum to “Optimization, modeling and accurate prediction of thermal conductivity and dynamic viscosity of stabilized ethylene glycol and water mixture Al2O3 nanofluids by NSGA-II using ANN” [Int. Commun. Heat Mass Transfer 82 :2017; 154–160]. Int Commun Heat Mass Transf 87:90. doi: https://doi.org/10.1016/j.icheatmasstransfer.2017.05.005
- Kim T, Heo J-H, Bae D-H, Kim J-H .Single-reservoir operating rules for a year using multiobjective genetic algorithm. J Hydroinformatics 2008; 10:163. doi: 10.2166/hydro.2008.019
- Chang LC, Chang FJ .Multi-objective evolutionary algorithm for operating parallel reservoir system. J Hydrol .2009; 377:12–20. doi: 10.1016/j.jhydrol.2009.07.061
- Shafii M, De Smedt F .Multi-objective calibration of a distributed hydrological model (WetSpa) using a genetic algorithm. Hydrol Earth Syst Sci Discuss .2009; 6:243–271. doi: 10.5194/hessd-6-243-2009
- Shiau J-T .Optimization of reservoir hedging rules using multiobjective genetic algorithm. J Water Resour Plan Manag 2009; 135:355–363. doi: 10.1061/(ASCE)0733-9496(2009)135:5(355)
- Esfe MH, Hajmohammad H, Moradi R, Arani AAA Multi-objective optimization of cost and thermal performance of double walled carbon nanotubes/water nanofluids by NSGA-II using response surface method. Appl Therm Eng .2017;112:1648–1657. doi: https://doi.org/10.1016/j.applthermaleng. 2016.10.129
- Horn J, Nafpliotis N, Goldberg DE .A niched Pareto genetic algorithm for multiobjective optimization. In: IEEE World Congress on Computational Intelligence. Orlando, FL.1994; 82–87
- Erickson M, Mayer A, Horn J .Multi-objective optimal design of groundwater remediation systems: Application of the niched Pareto genetic algorithm (NPGA). Adv Water Resour .2002; 25:51–65. doi: 10.1016/S0309-1708(01)00020-3
- Chen L, McPhee J, Yeh WWG .A diversified multiobjective GA for optimizing reservoir rule curves. Adv Water Resour .2007; 30:1082–1093. doi: 10.1016/j.advwatres.2006.10.001
- Marin J, Sole R .Macroevolutionary algorithms: a new optimization method on fitness landscapes. IEEE Trans Evol Comput .1999; 3:272–286. doi: 10.1109/4235.797970
- Gaspar-Cunha A. Modelling and optimisation of single screw extrusion - using multi-objective evolutionary algorithms. Universidade do Minho 1999.
- da Cunha AGL, Covas JACG .RPSGAe -reduced Pareto set genetic algorithm: application to polymer extrusion. Metaheuristics Multiobjective Optim .2004; 221–249.
- Yapo PO, Gupta H V, Sorooshian S .Multi-objetive global optimization for hydrologic models. J Hydrol .1998; 204:83–97. doi: 10.1016/S0022-1694(97)00107-8
- Beldring S .Multi-criteria validation of a precipitation-runoff model. J Hydrol .2002; 257:189–211. doi: 10.1016/S0022-1694(01)00541-8ds
- Gupta H V, Bastidas LA, Vrugt A. Multiple criteria global optimization for watershed. Water Sci Appl. 2003; 6:125–132.
- Vrugt JA, Gupta HV, Bastidas LA. Effective and efficient algorithm for multiobjective optimization of hydrologic models. Water Resour Res. 2003; 39:1-19. doi: 10.1029/2002WR001746
- Moore J, Chapman R. Application of particle swarm to multiobjective optimization. 1999.
- Kennedy J, Eberhart R. Particle swarm optimization. Proc 1995 IEEE Int Conf Neural Networks Part 1 (of 6). 1995; 4:1942–1948. doi: 10.1007/s11721-007-0002-0
- Raquel CR, Naval PC. An effective use of crowding distance in multiobjective particle swarm optimization. In: Proceedings of the 2005 conference on Genetic and evolutionary computation. 2005; 257–264
- Sierra MR, Coello CC. Improving PSO-based multi-objective optimization using crowding, mutation and ε-dominance. In: Evolutionary Multi-Criterion Optimization. 2005; 505–519.
- Moradi AM, Dariane AB. Particle Swarm Optimization: Application to Reservoir Operation Problems. In: Advance Computing Conference. IEEE International, Patiala, India, 2009.
- Reddy MJ, Kumar ND. Multi-objective particle swarm optimization for generating optimal trade-offs in reservoir operation. Hydrol Process. 21: 2897-2909. doi: 10.1002/hyp.6507
- Elhossini A, Areibi S, Dony R. Strength Pareto particle swarm optimization and hybrid EA-PSO for multi-objective optimization. Evol Comput. 2010 Spring;18(1):127-56. doi: 10.1162/evco.2010.18.1.18105. PMID: 20064026.
- Goh CK, Tan KC, Liu DS, Chiam SC. A competitive and cooperative co-evolutionary approach to multi-objective particle swarm optimization algorithm design. Eur J Oper Res. 2010; 202:42–54. doi: 10.1016/j.ejor.2009.05.005
- Ding S, Chen C, Xin B, Pardalos PM. A bi-objective load balancing model in a distributed simulation system using NSGA-II and MOPSO approaches. Appl Soft Comput. 2018; 63:249–267. doi: https://doi.org/10.1016/j.asoc.2017.09.012
- Lin YH, Huang LC, Chen SY, Yu CM. The optimal route planning for inspection task of autonomous underwater vehicle composed of MOPSO-based dynamic routing algorithm in currents. Appl Ocean Res. 2018; 75:178–192. doi: https://doi.org/10.1016/j.apor.2018.03.016
- Nazemzadegan MR, Kasaeian A, Toghyani S. Multi-objective optimization in a finite time thermodynamic method for dish-Stirling by branch and bound method and MOPSO algorithm. Front Energy. 2018. doi: 10.1007/s11708-018-0548-0
- Briza AC, Naval PC. Stock trading system based on the multi-objective particle swarm optimization of technical indicators on end-of-day market data. Appl Soft Comput. 2011; 11:1191–1201. doi: 10.1016/j.asoc.2010.02.017
- Qasem SN, Shamsuddin SM. Radial basis function network based on time variant multi-objective particle swarm optimization for medical diseases diagnosis. Appl Soft Comput. 2011; 11:1427–1438. doi: 10.1016/j.asoc.2010.04.014
- Sun X, Chen Y, Liu Y, Gong D. Indicator-based set evolution particle swarm optimization for many-objective problems. Soft Comput. 2015. doi: 10.1007/s00500-015-1637-1
- Huang V, Suganthan P, Liang J. Comprehensive learning particle swarm optimizer for solving multi-objective optimization problems. Int J Intell Syst. 2006; 10:281–295. doi: 10.1109/TEVC.2005.857610
- Motameni H. PSO for multi-objective problems : Criteria for leader selection and uniformity distribution. J AI Data Min. 2016; 4:67–76.
- Li X. A non-dominated sorting particle swarm optimizer for multi-objective optimization. In: Genetic and Evolutionary Computation — GECCO. 2013; 37-48.
- Mostaghim S, Teich J. Strategies for finding good local guides in multi- objective particle swarm optimization (MOPSO). In: Swarm Intelligence Symposium, 2003. SIS ’03. Proceedings of the 2003 IEEE. 26–33.
- Toscano Pulido G, Coello Coello CA. Using clustering techniques to improve the performance of a multi-objective particle swarm optimizer. In: Genetic and Evolutionary Computation – GECCO 2004; 225–237.
- Coello C, Reyes-Sierra M. Multi-objective particle swarm optimizers: a survey of the state-of-the-art. Int J Comput Intell Res. 2006; 2:287–308. doi: 10.5019/j.ijcir.2006.68
- Gad AG. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Archives of Computational Methods in Engineering. 2022; 1-31.
- Hadka D, Reed P. Borg: an auto-adaptive many-objective evolutionary computing framework. Evol Comput. 2013 Summer;21(2):231-59. doi: 10.1162/EVCO_a_00075. Epub 2012 Apr 9. PMID: 22385134.
- Laumanns M, Thiele L, Deb K, Zitzler E. Combining convergence and diversity in evolutionary multiobjective optimization. Evol Comput. 2002 Fall;10(3):263-82. doi: 10.1162/106365602760234108. PMID: 12227996.
- Tang Y, Reed PM, Kollat JB. Parallelization strategies for rapid and robust evolutionary multiobjective optimization in water resources applications. Adv Water Resour. 2007; 30:335–353. doi: 10.1016/j.advwatres.2006.06.006
- Jingfeng Y, Meilian L, Zhijie X. A simple Pareto adaptive -domination differential evolution algorithm for multi-objective optimization. Open Autom Control Syst J. 2015; 7:338–345.
- Hernández-Díaz AG, Santana-Quintero LV, Coello Coello CA, Molina J. Pareto-adaptive epsilon-dominance. Evol Comput. 2007 Winter;15(4):493-517. doi: 10.1162/evco.2007.15.4.493. PMID: 18021017.
- Storn R, Price K. Differential evolution - A simple and efficient adaptive scheme for global optimization over continuous spaces. Tech Rep 1995; -95-012:1–12.
- Storn R, Price K. Home page of differential evolution. 2003. http://www1.icsi.berkeley.edu/~storn/code.html.
- Kukkonen S, Lampinen J. An extension of generalized differential evolution for multi-objective optimization with constraints. In: 8th International Conference on Parallel Problem Solving from Nature (PPSN). Springer, Berlin. 2004; 752–761
- Santana-Quintero LV, Coello C. An algorithm based on differential evolution for multi-objective problems. Int J Comput Intell Res. 2005; 1:151–169. doi: 10.5019/j.ijcir.2005.32
- Alatas B, Akin E, Karci A. MODENAR: Multi-objective differential evolution algorithm for mining numeric association rules. Appl Soft Comput J. 2008; 8:646–656. doi: 10.1016/j.asoc.2007.05.003
- Qu B, Suganthan PN. Multi-objective differential evolution with diversity enhancement. J Zhejiang Univ C. 2010; 11:538–543. doi: 10.1631/jzus.C0910481
- Sarker R, Abbass HA. Differential evolution for solving multi-objective optimization problems. Asia-Pacific J Oper Res. 2003; 21:1–20.
- Raad D, Sinske A, van Vuuren J. Robust multi-objective optimization for water distribution system design using a meta-metaheuristic. Int Trans Oper Res. 2009; 16:595–626. doi: 10.1111/j.1475-3995.2009.00705.x
- Gong W, Cai Z. An improved multiobjective differential evolution based on Pareto-adaptive ε{lunate}-dominance and orthogonal design. Eur J Oper Res. 2009; 198:576–601. doi: 10.1016/j.ejor.2008.09.022
- Cai ZH, Gong WY, Huang YQ. A novel differential evolution algorithm based on ε-domination and orthogonal design method for multi-objective optimization. In: Fourth International Conference on Evolutionary Multi-Criterion Optimization (EMO-07). 2007; 286–301.
- Ariyasingha IDID, Fernando TGI. Performance analysis of the multi-objective ant colony optimization algorithms for the traveling salesman problem. Swarm Evol Comput. 2005; 23:11–26. doi: 10.1016/j.swevo.2015.02.003
- Huang RH, Yu TH. An effective ant colony optimization algorithm for multi-objective job-shop scheduling with equal-size lot-splitting. Appl Soft Comput. 2017; 57:642–656. doi: https://doi.org/10.1016/j.asoc.2017.04.062
- Hajibandeh E, Nazif S. Pressure Zoning Approach for Leak Detection in Water Distribution Systems Based on a Multi Objective Ant Colony Optimization. Water Resour Manag. 2018; 32:2287–2300. doi: 10.1007/s11269-018-1929-1
- Baran B, Schaerer M. A multiobjective ant colony system for vehicle routing problem with time windows. In: The 21st International Conference Applied Informatics. Innsbruck, Austria. 2003; 97–102.
- Dariane AB, Moradi AM. Reservoir Operating by Ant Colony Optimization for Continuous Domains (ACOR) Case Study: Dez Reservoir. Int J Civil, Environ Struct Constr Archit Eng. 2008; 2:136–140.
- Zhou J, Wang C, Li Y. A multi-objective multi-population ant colony optimization for economic emission dispatch considering power system security. Appl Math Model. 2017; 45:684–704. doi: https://doi.org/10.1016/j.apm.2017.01.001
- Mariano C, Morales E. A multiple objective ant-q algorithm for the design of water distribution irrigation networks. 1999.
- Schlünz EB, Bokov PM, van Vuuren JH. A comparative study on multiobjective metaheuristics for solving constrained in-core fuel management optimisation problems. Comput Oper Res. 2016; 75:174–190. doi: 10.1016/j.cor.2016.06.001
- Mokhtari N, Ghezavati V. Integration of efficient multi-objective ant-colony and a heuristic method to solve a novel multi-objective mixed load school bus routing model. Appl Soft Comput. 2018; 68:92–109. doi: https://doi.org/10.1016/j.asoc.2018.03.049
- Golding P, Kapadia S, Naylor S. Framework for minimising the impact of regional shocks on global food security using multi-objective ant colony optimisation. Environ Model Softw. 2017; 95:303–319. doi: https://doi.org/10.1016/j.envsoft.2017.06.004
- Zhao B, Gao J, Chen K, Guo K. Two-generation Pareto ant colony algorithm for multi-objective job shop scheduling problem with alternative process plans and unrelated parallel machines. J Intell Manuf. 2018; 29:93–108. doi: 10.1007/s10845-015-1091-z
- Vrugt JA, Robinson BA. Improved evolutionary optimization from genetically adaptive multi-method search. In: National Academy of Sciences. USA, 2007; 708–711
- Ouyang Q, Lu W, Hou Z, Zhang Y, Li S, Luo J. Chance-constrained multi-objective optimization of groundwater remediation design at DNAPLs-contaminated sites using a multi-algorithm genetically adaptive method. J Contam Hydrol. 2017 May;200:15-23. doi: 10.1016/j.jconhyd.2017.03.004. Epub 2017 Mar 14. PMID: 28363342.
- Zitzler E, Thiele L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans Evol Comput. 1999; 3:257–271.
- Rudziński F. An Application of Generalized Strength Pareto Evolutionary Algorithm for Finding a Set of Non-Dominated Solutions with High-Spread and Well-Balanced Distribution in the Logistics Facility Location Problem. In: Rutkowski L, Korytkowski M, Scherer Rafałand Tadeusiewicz R, et al. (eds) Artificial Intelligence and Soft Computing. Springer International Publishing, Cham. 2017; 439–450
- Yuan X, Zhang B, Wang P. Multi-objective optimal power flow based on improved strength Pareto evolutionary algorithm. Energy. 2017; 122:70–82. doi: https://doi.org/10.1016/j.energy.2017.01.071
- Marrouche W, Farah R, Harmanani HM. A Multiobjective Optimization Method for the SOC Test Time, TAM, and Power Optimization Using a Strength Pareto Evolutionary Algorithm. In: Latifi S (ed) Information Technology - New Generations. Springer International Publishing, Cham. 2018; 685-695.
- Zitzler E, Laumanns M, Thiele L. SPEA2: Improving the strength pareto evolutionary algorithm. Evol Methods Des Optim Control with Appl to Ind Probl. 2001; 95–100. doi: 10.1.1.28.7571
- Knowles JD, Corne DW. Approximating the nondominated front using the Pareto Archived Evolution Strategy. Evol Comput. 2000 Summer;8(2):149-72. doi: 10.1162/106365600568167. PMID: 10843519.
- Corne DW, Knowles JD, Oates MJ. The Pareto envelope-based selection algorithm for multi-objective optimization. In: the Sixth International Conference on Parallel Problem Solving from Nature. 2000; 839–848.
- Peng X, Xia X, Liao W, Guo Z. Running time analysis of the Pareto archived evolution strategy on pseudo-Boolean functions. Multimed Tools Appl. 2018; 77:11203–11217. doi: 10.1007/s11042-017-5466-3
- Wagner T, Beume N, Naujoks B. Pareto-, Aggregation-, and Indicator-Based Methods in Many-Objective Optimization. In: Obayashi S, Deb K, Poloni C, et al. (eds) Evolutionary Multi-Criterion Optimization: 4th International Conference, EMO 2007, Matsushima, Japan, March 5-8, 2007. Proceedings. Springer Berlin Heidelberg, Berlin, Heidelberg, 2007; 742–756.
- Ishibuchi H, Tsukamoto N, Nojima Y. Evolutionary many-objective optimization: A short review. In: Evolutionary Computation, 2008. CEC 2008. (IEEE World Congress on Computational Intelligence). IEEE Congress on.
- Li M, Yang S, Liu X, Shen R. A Comparative Study on Evolutionary Algorithms for Many-Objective Optimization. In: Purshouse RC, Fleming PJ, Fonseca CM, et al. (eds) Evolutionary Multi-Criterion Optimization: 7th International Conference, EMO 2013, Sheffield, UK, March 19-22, 2013. Proceedings. Springer Berlin Heidelberg, Berlin, Heidelberg 2013; 261–275.
- Walker DJ, Everson RM, Fieldsend JE. Visualizing mutually nondominating solution sets in many-objective optimization. IEEE Trans Evol Comput. 2013; 17:165–184. doi: 10.1109/TEVC.2012.2225064
- Tusar T, Filipic B. Visualization of Pareto front approximations in evolutionary multiobjective optimization: a critical review and the prosection method. IEEE Trans Evol Comput. 2015; 19:225–245. doi: 10.1109/TEVC.2014.2313407
- Brockhoff D, Zitzler E. Objective reduction in evolutionary multiobjective optimization: theory and applications. Evol Comput. 2009; 17:135–166. doi: 10.1162/evco.2009.17.2.135
- Singh HK, Isaacs A, Ray T. Dimensionality Reduction in Many-Objective Optimization Problems. IEEE Trans Evol Comput. 2011; 15:539–556.
- Saxena D, Duro J, Tiwari A. Objective reduction in many-objective optimization: linear and nonlinear algorithms. IEEE Trans Evol Comput. 2013; 17:77–99.
- Bandyopadhyay S, Mukherjee A. An algorithm for many-objective optimization with reduced objective computations: A study in differential evolution. IEEE Trans Evol Comput. 2015; 19:400–413. doi: 10.1109/TEVC.2014.2332878
- Zhou Y, Wang J, Chen J. Ensemble of many-objective evolutionary algorithms for many-objective problems. Soft Comput. 2017; 21:2407–2419. doi: 10.1007/s00500-015-1955-3
- Steponavič\.e I, Hyndman RJ, Smith-Miles K, Villanova L. Dynamic algorithm selection for pareto optimal set approximation. J Glob Optim. 2016; 1–20. doi: 10.1007/s10898-016-0420-x
- Zitzler E, Thiele L. Multi-objective optimization using evolutionary algorithms- a comparative case study. In: Parallel Problem Solving from Nature — PPSN V. 1998; 292–301
- Emmerich M, Beume N, Naujoks B. An EMO algorithm using the hypervolume measure as selection criterion. In: Evolutionary Multi-Criterion Optimization. 2000; 32–76.
- Zitzler E, Künzli S. Indicator-based selection in multiobjective search. In: Parallel Problem Solving from Nature - PPSN VIII. 2004; 832–842.
- Beume N, Naujoks B, Emmerich M .SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur J Oper Res. 2007; 181:1653–1669. doi: 10.1016/j.ejor.2006.08.008
- Brockhoff D, Zitzler E .Improving hypervolume-based multiobjective evolutionary algorithms by using objective reduction methods. In: Congress on Evolutionary Computation (CEC). 2007; 2086–2093
- Igel C, Hansen N, Roth S. Covariance matrix adaptation for multi-objective optimization. Evol Comput. 2007 Spring;15(1):1-28. doi: 10.1162/evco.2007.15.1.1. PMID: 17388777.
- Yuan Y, Xu H, Wang B. Balancing convergence and diversity in decomposition-based many-objective optimizers. IEEE Trans Evol Comput .2016; 20:180–198. doi: 10.1109/TEVC.2015.2443001
- Yuan Y, Xu H, Wang B, Yao X .A new dominance relation-based evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput .2016; 20:16–37. doi: 10.1109/TEVC.2015.2420112
- Bader J, Zitzler E. HypE: an algorithm for fast hypervolume-based many-objective optimization. Evol Comput. 2011 Spring;19(1):45-76. doi: 10.1162/EVCO_a_00009. Epub 2010 Jul 22. PMID: 20649424.
- Zitzler E, Brockhoff D, Thiele L .The hypervolume indicator revisited: on the design of Pareto-compliant indicators via weighted integration. Evol Multi-Criterion Optim. 2007;l4403:862–876. doi: 10.1007/978-3-540-70928-2_64
- Jiang S, Zhang J, Ong YS, Zhang AN, Tan PS. A Simple and Fast Hypervolume Indicator-Based Multiobjective Evolutionary Algorithm. IEEE Trans Cybern. 2015 Oct;45(10):2202-13. doi: 10.1109/TCYB.2014.2367526. Epub 2014 Dec 2. PMID: 25474815.
- Yang S, Li M, Liu X, Zheng J .A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput .2013;17:721–736. doi: 10.1109/TEVC.2012.2227145
- Deb K, Jain H .An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach, Part II: handling constraints and extending to an adaptive approach. IEEE Trans Evol Comput .2013; 18:602–622. doi: 10.1109/TEVC.2013.2281534
- Ruiz AB, Saborido R, Luque M .A preference-based evolutionary algorithm for multiobjective optimization: the weighting achievement scalarizing function genetic algorithm. J Glob Optim .2015; 62:101–129. doi: 10.1007/s10898-014-0214-y
- Li Y, Liu H, Xie K, Yu X .A method for distributing reference points uniformly along the Pareto front of DTLZ test functions in many-objective evolutionary optimization. 2015 5th Int Conf Inf Sci Technol ICIST 2015 ;541–546. doi: 10.1109/ICIST.2015.7289031
- Seada H, Deb K .U-NSGA-III: A unified evolutionary optimization procedure for single, multiple, and many objectives: proof-of-principle results. In: Evolutionary Multi-Criterion Optimization. 2015; 34–49
- Yi J-H, Deb S, Dong J. An improved NSGA-III algorithm with adaptive mutation operator for Big Data optimization problems. Futur Gener Comput Syst.2018; 88:571–585. doi: https://doi.org/10.1016/j.future.2018.06.008
- Zhu Y, Liang J, Chen J, Ming Z .An improved NSGA-III algorithm for feature selection used in intrusion detection. Knowledge-Based Syst .2017; 116:74–85. doi: https://doi.org/10.1016/j.knosys.2016.10.030
- Gonçalves RA, Pavelski LM, de Almeida CP. Adaptive Operator Selection for Many-Objective Optimization with NSGA-III. In: Trautmann H, Rudolph G, Klamroth K, .(eds) Evolutionary Multi-Criterion Optimization. Springer International Publishing, Cham. 2017; 267–281
- Tanabe R, Oyama A .The Impact of Population Size, Number of Children, and Number of Reference Points on the Performance of NSGA-III. In: Trautmann H, Rudolph G, Klamroth K.(eds) Evolutionary Multi-Criterion Optimization. Springer International Publishing, Cham.2017; 606–621
- Wu HC .A Solution Concept for Fuzzy Multiobjective Programming Problems Based on Convex Cones. J Optim Theory Appl .2004; 121:397–417. doi: 10.1023/B:JOTA.0000037411.25509.6a
- Wu HC .Solutions of Fuzzy Multiobjective Programming Problems Based on the Concept of Scalarization. J Optim Theory Appl 2008; 139:361–378. doi: 10.1007/s10957-008-9419-x
- Nasir M, Mondal A, Sengupta S.An improved multi-objective evolutionary algorithm based on decomposition with fuzzy dominance. In: the IEEE Congress on Evolutionary Computation. New Orleans, LA, 2011; 765–772
- Eshtehardian E, Afshar A, Abbasnia R .Fuzzy-based MOGA approach to stochastic time–cost trade-off problem. Autom Constr 2009; 18:692–701. doi: 10.1016/j.autcon.2009.02.001
- Gong D, Wang G, Sun X, Han Y .A set-based genetic algorithm for solving the many-objective optimization problem. Soft Comput .2015; 19:1477–1495. doi: 10.1007/s00500-014-1284-y
- Zhu C, Xu L, Goodman ED . Generalization of Pareto-optimality for many-objective evolutionary optimization. IEEE Trans Evol Comput .2016;20:299–315. doi: 10.1109/TEVC.2015.2457245
- Ikeda I, Kita H, Kobayashi S .Failure of Pareto-based MOEAs: does nondominated really mean near to optimal. Seoul.2001; 957–962 vol. 2
- Dai C, Wang Y, Hu L .An improved (Formula presented.) -dominance strategy for many-objective optimization problems. Soft Comput .2016; 20:1105–1111. doi: 10.1007/s00500-014-1570-8
- Zhang Q, Li H .MOEA/D: A multiobjective evolutionary algorithm based on decomposition. Evol Comput IEEE Trans. 2007; 11:712–731. doi: 10.1109/TEVC.2007.892759
- Asafuddoula M, Ray T, Ruhul S .A decomposition based evolutionary algorithm for many-objective optimization with systematic sampling and adaptive epsilon control. In: Evolutionary Multi-Criterion Optimization. 2013; 413–427
- Asafuddoula M, Ray T, Sarker R .A decomposition-based evolutionary algorithm for many objective optimization. IEEE Trans Evol Comput .2015; 19:445–460. doi: 10.1109/TEVC.2014.2339823
- Karami F, Dariane AB Many-Objective Multi-Scenario Algorithm for Optimal Reservoir Operation Under Future Uncertainties. Water Resour Manag. doi: 10.1007/s11269-018-2025-2 ,2018.
- Srdjevic B .Linking analytic hierarchy process and social choice methods to support group decision-making in water management. Decis Support Syst .2007; 42:2261–2273. doi: 10.1016/j.dss.2006.08.001
- Ebert U, Welsch H .Meaningful environmental indices: A social choice approach. J Environ Econ Manage .2004; 47:270–283. doi: 10.1016/j.jeem.2003.09.001
- Huband S, Hingston P, Barone L, While L (2006) A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans Evol Comput .2006; 10:477–506. doi: 10.1109/TEVC.2005.861417
- Ishibuchi H, Setoguchi Y, Masuda H, Nojima Y .Performance of Decomposition-Based Many-Objective Algorithms Strongly Depends on Pareto Front Shapes. IEEE Trans Evol Comput .2017;21:169–190. doi: 10.1109/TEVC.2016.2587749
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
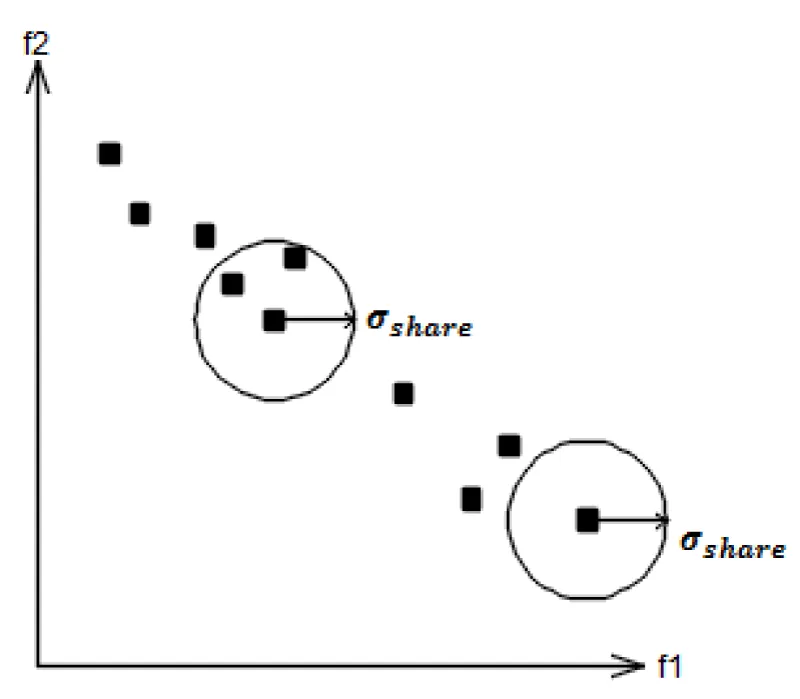
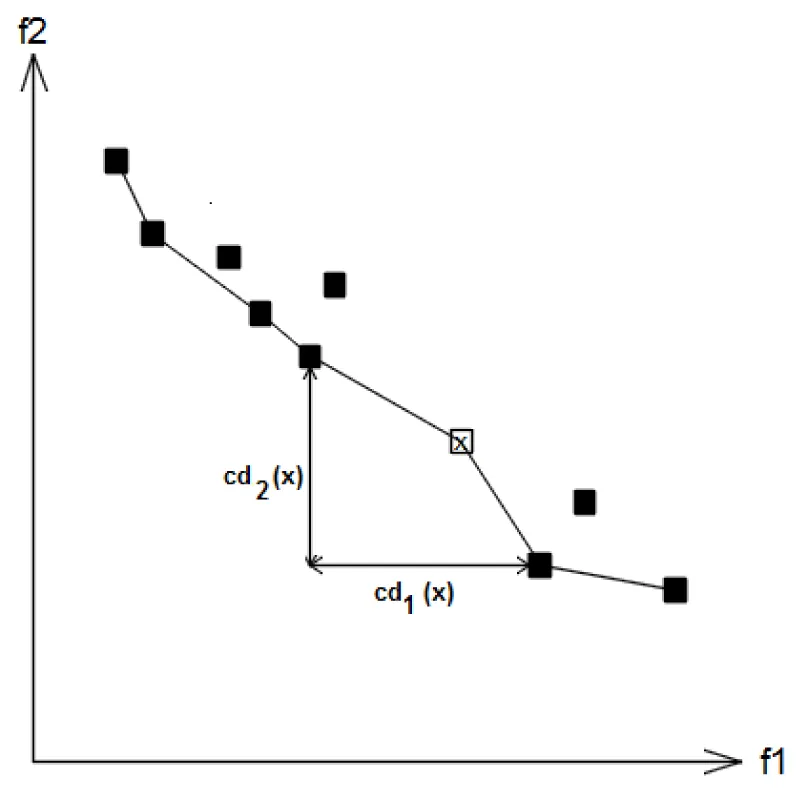
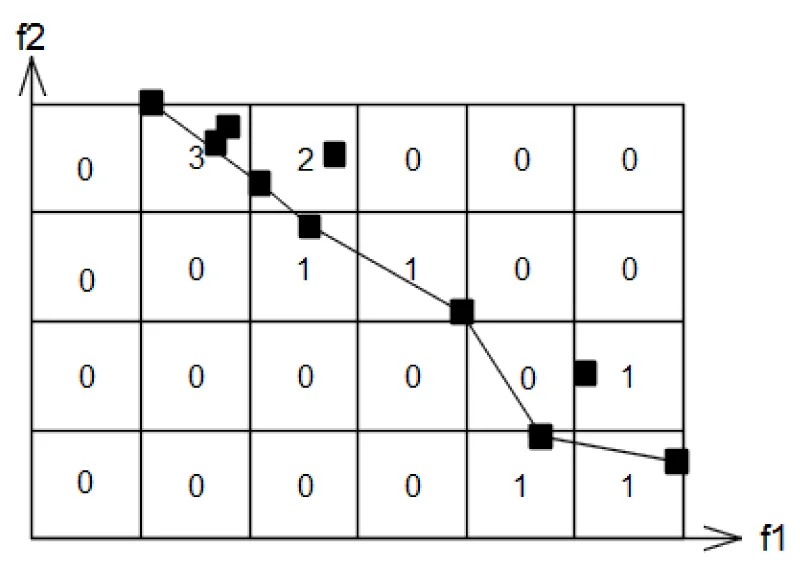
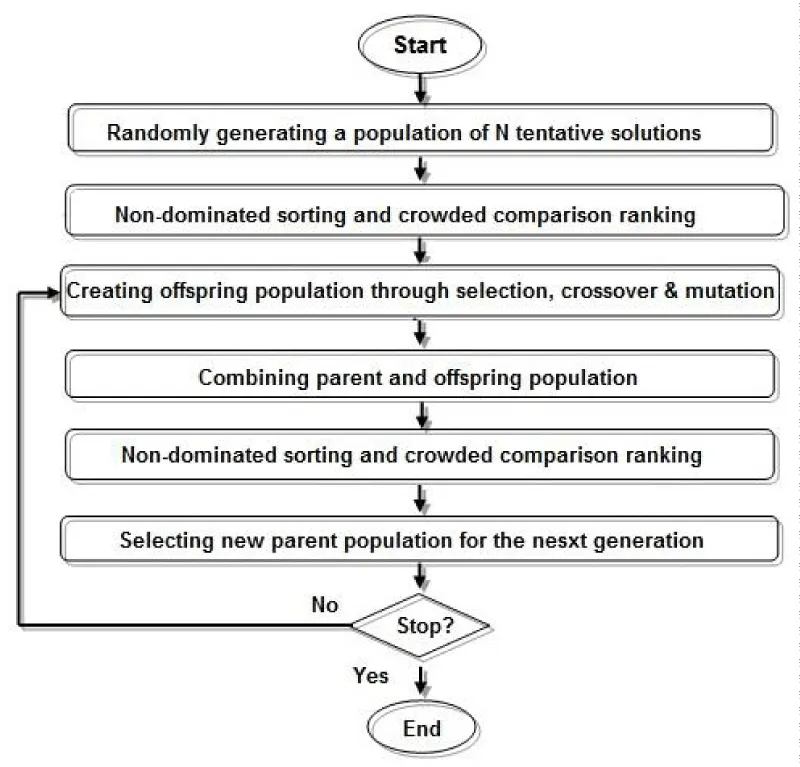
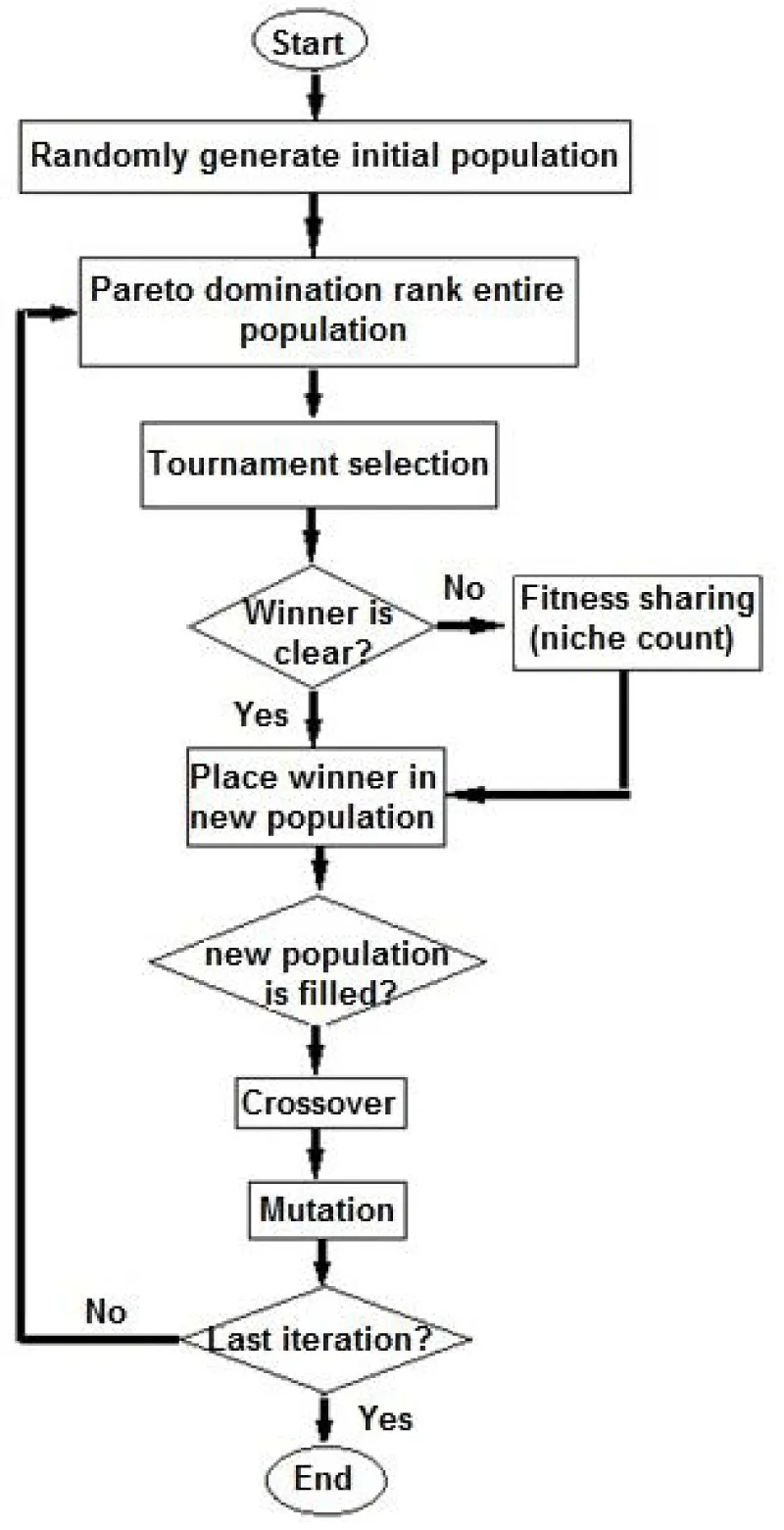
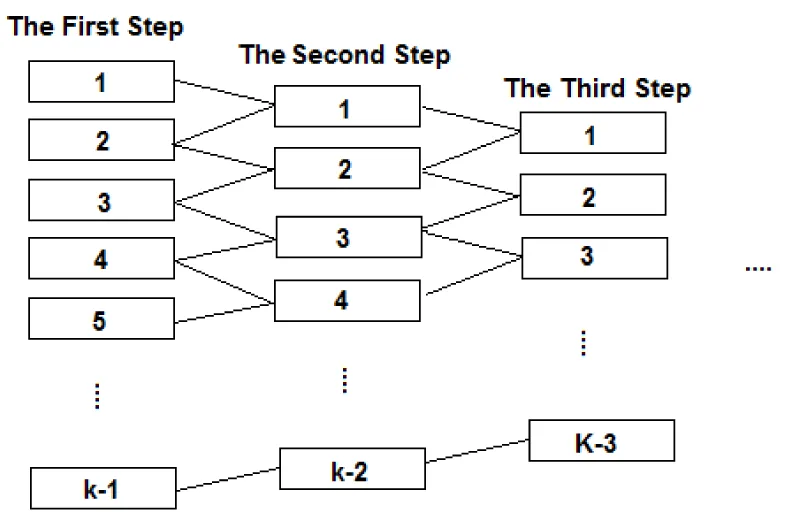
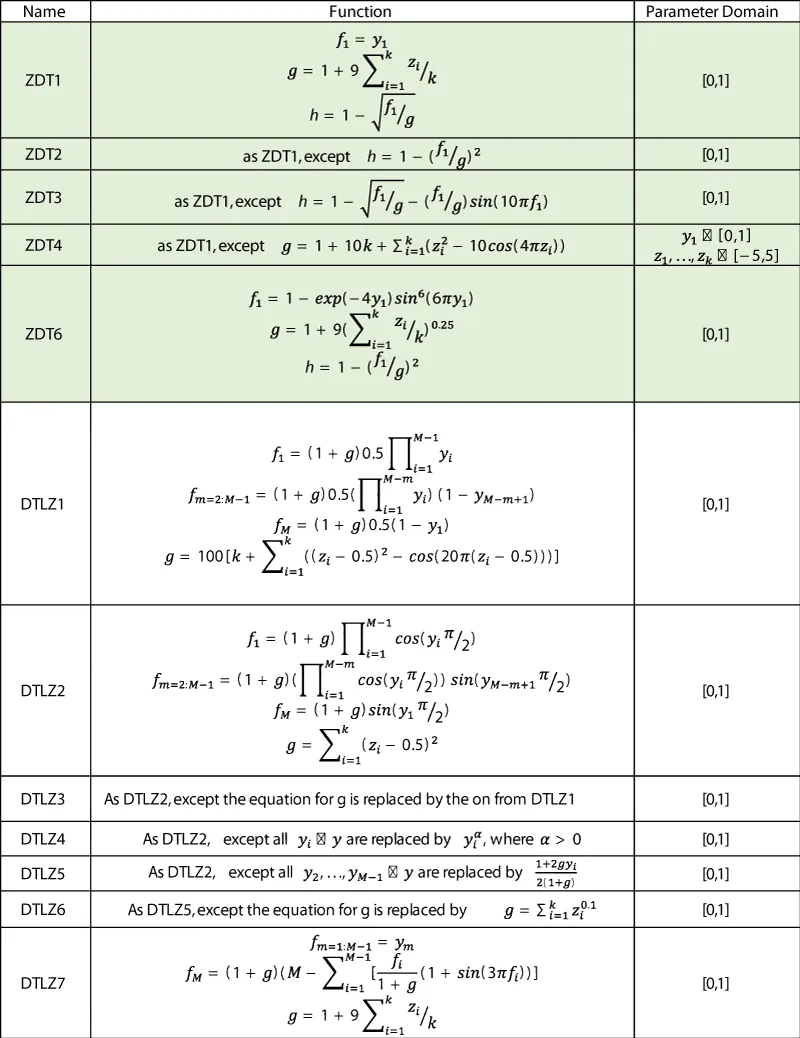


 Save to Mendeley
Save to Mendeley
