Eco-evolutionary dynamics of intergenomic epistatic QTLs under slight and hard multilevel selections in community genetics

Eco-evolutionary community genetics refers to the study of population genetics at multispecies levels since a single species evolves genetically through interactions with other species. The aim of this paper is dynamical modeling of interspecific quantitative trait loci (QTL) under slight and hard multilevel selection to investigate eco-evolutionary genetic relationships among QTL of multispecies. It was found that the simplex ${\Im }_{\theta }$ explained the intergenomic epistatic QTL (IEQ) dynamics in a discrete-time model according to Wright’s manifold. Besides, the generalized $\nabla$ gradient system on the simplex ${\Im }_{\theta }$ demonstrated the IEQ dynamics in a continuous-time model. The outcomes of slight and hard multilevel selection on the expressions of IEQ in species were explained by the gradient operator of the mean multilevel fitness. IEQ analysis was integrated into community genetics according to Lande’s assumptions, so for slight multilevel selection, the geometric average of the mean multilevel fitness specified Wright’s idea of adaptive topography. The dynamical system for phenotypic eco-evolution under a hard multilevel selection gradient was studied and the relative mean multilevel fitness of two species was estimated.

Introduction

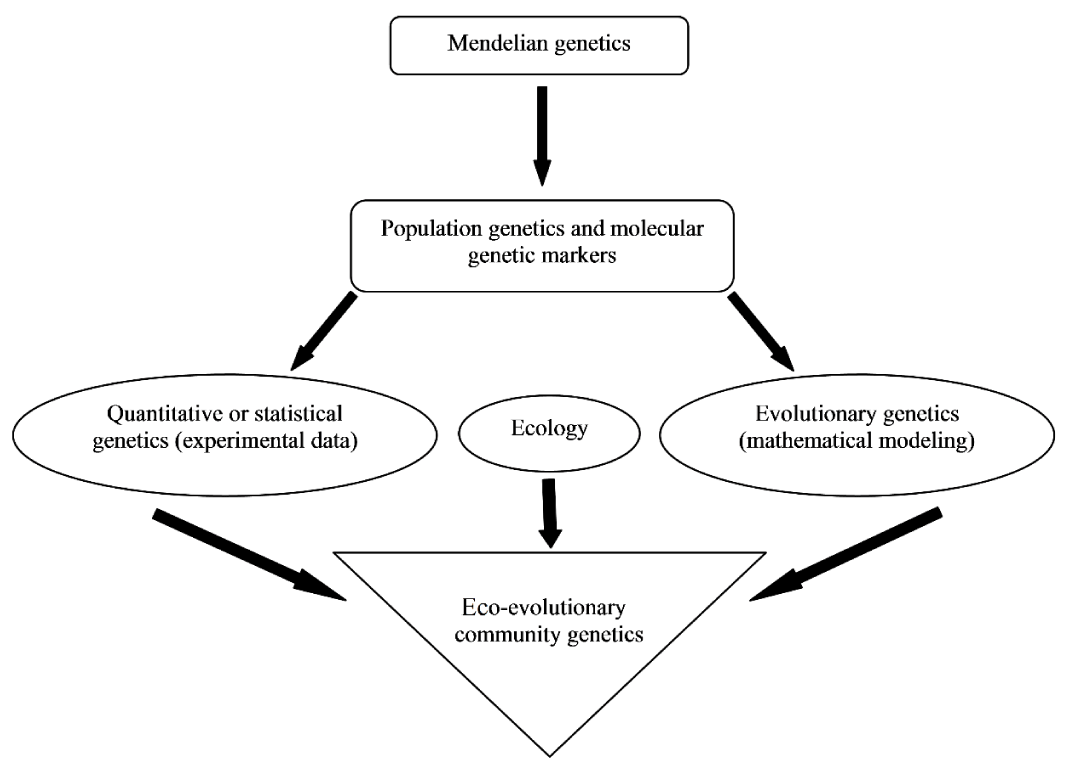
The elementary theory of genetics was proposed by Mendel in 1865 as the disjoined inheritance of seed shape of common pea plants, and eye color of Drosophila by which he explained the variations in natural populations. Mendel had also proposed the three principles of inheritance that determined the transfer of genetic characters among successive generations [1]. Therefore, Mendelian genetics became the basis for population genetics studies (Figure 1).

Figure 1: Relationship between Mendelian and population genetics, plus connections among multivariate quantitative genetics, evolutionary genetics, and ecology such that the triangle of eco-evolutionary community genetics arises.

Then, the Mendelian factors were applied to explain the genetic control of complex and continuous characters. Darwin explained that the genetic interactions among the individuals of the community promoted the biodiversity of species and their adaptation to habitat [2]. Population and quantitative genetics integrate Mendel’s laws, statistical models, and other genetic rules to study the inheritance of complex traits in relation to population structure, whereas community genetics expands these rules too complicated and interconnected communities [3]. With the advancement of molecular marker technologies, QTL mapping and genome-wide association study (GWAS) based on genetic linkage and linkage disequilibrium (LD) maps are used to analyze complex characters inheritance in artificial and natural populations [4].

In population genetics, the coefficients of multivariate selection are considered fixed parameters, but obviously, they are not reliable in community genetics because the living populations are interconnected to create the natural complicated multispecies communities in variable habitats. These populations are developed under abiotic and biotic stress conditions in different environments, but these conditions are usually not fully investigated in models of mathematical population genetics [5].

In genetic studies, theoretical modeling of different problems is investigated by mathematical procedures, whereas statistical methods perform inferences from experimental genetic data. Both quantitative and evolutionary genetics has founded on population genetics, but as Figure 1 shows, the eco-evolutionary community genetics integrates quantitative and evolutionary genetics with ecology. In other words, community genetics aims to study population genetics at higher levels, i.e., at the multispecies level although there is not enough research about different evolutionary processes on ecosystems [6].

Community genetics studies were triggered through ecological genetic investigations by Dobzhansky [7] and Ford [8] by integrating population genetics, multilevel selection, and eco-evolutionary responses [8]. Therefore, community ecology and population genetics needed to be assessed together [9,10]. A community is defined as similar species that are joined together through a gene reservoir, where the interactions among species that are existed in a similar environment are developed in connections to other species. Community genetics was introduced to explain the fact that genetic evolution in a single species might be determined by other species in the community. To introduce a new branch of biosciences, the complete integration of genetics and ecology, called community genetics, was recommended by Neuhauser et al. [12] and Whitham et al. [3].

Community genetics has often been used for investigating the genetic changes in terrestrial foundation plants, and sometimes higher trophic levels [13]. In ecosystem studies, the foundation species term is applied to a species that has a major duty in constructing a community. These species can settle at any trophic level in a food cycle. In foundation species, the genetic variation is linked to other species existing in the community, according to the Whitham et al. [3] theory. But Neuhauser et al. [12] proposed that hard multilevel selection could act on communities that had partitioned genetically. Therefore, a QTL belonging to a foundation species can influence phenotypes of other species living in the community which is called community epistasis. This subject needs to assess QTL in a specific scientific method, instead of the usual procedures in QTL mappings [3].

According to community genetics, genetic changes in one species affect the other members of the community, therefore mean multilevel fitness of the community is arisen due to eco-evolutionary responses to multilevel selection [14]. In other words, the species are not independent of each other, but they live in a context including interrelations of thousands of organisms in varying habitats. Therefore, community genetics gives special importance to the study of eco-evolutionary genetic processes happening among the interrelating populations in the communities [3]. Community genetics is explained by interspecific genetic systems based on intraspecific genetic networks [15].

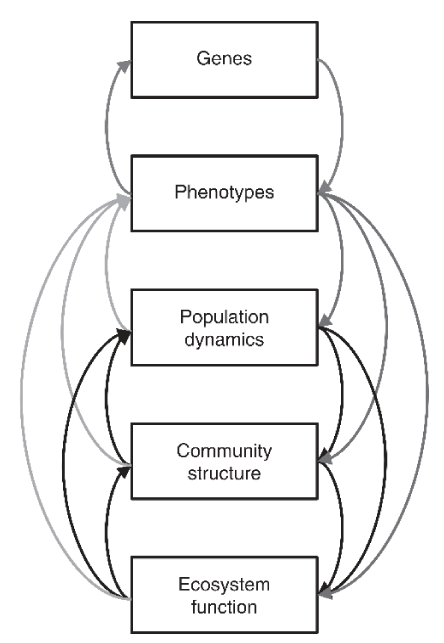
At the population genetics level, evolutionary adaptation changes the population size, but at the community genetics level, interspecific interactions affect the community. On the other hand, at the ecosystem level, interspecific variations affect the reproduction of the community (Figure 2) [16].

Figure 2: Different levels of interspecific relationships in the eco-evolutionary community. Phenotypic characters in a focal species act on the dynamics of population genetics, community, and ecosystem. Also, the variations at population, community, and ecosystem levels influence the phenotypic characters. Figure reproduced with permission from REF. Hendry, © (2013) Macmillan Publishers Limited.

Community genetics explains how genetic co-variation within populations affects the genetic diversity of species within communities, and how interrelations of species affect the direction of co-evolution [17,18]. The unification of genetics and ecology merges the macro-evolutionary and micro-evolutionary activities in community genetics, even in agricultural communities [19].

A lot of genes interact together and with habitat, therefore eco-evolutionary dynamics of QTL is depended on the interrelations between genetic and habitat factors. The relationship between the quantitative traits and DNA sequences helps to predict diseases and suitable treatments in human communities and to improve the mechanisms of adaptive eco-evolution in animals and plants [20]. The sources of variations in community genetics are classified into four categories: i) variations within populations, ii) variations among populations, iii) variations within species and iv) variations among species. QTL analysis is applied to a) identify a part of a chromosome including one or several loci that are influenced by a character in a particular habitat, b) evaluate the number of genes, their size, and effect as positive or negative, c) study of gene actions as additive, dominance or overdominance effects, and d) investigate gene interactions as epistatic effects [3]. Since eco-evolutionary dynamics of complex traits (for example in agriculture, medicine, and biology) are managed by a large number of genes and their interactions with habitat, therefore functional mapping is needed to study eco-evolutionary dynamics in community genetics [21].

In some studies on insect species, significant broad-sense co-heritabilities were reported among insect species such that many genomic areas across several linkage groups (determined by QTL analyses) were common to insect genomes living in a community. As well in the natural Populus communities, plant genotypes could anticipate arthropods genomes in their community. This community was affected by the frequency of invertebrates and their airborne predators and was under the influence of soil bacterial community too. Therefore, it was revealed that community consistency had a genetic basis since these models of community relationships were heritable and stable across years. It was shown that plant phenology could be useful for community genetics studies [22].

Eco-evolutionary geneticists have struggled a lot to perceive complex processes that have caused genetic changes in communities. Genome-wide association studies based on high-level polymorphisms at the molecular level have been used to explain eco-evolutionary processes that could make the variations. Knowledge about the genetic structures of QTL alleles is necessary for understanding eco-evolutionary processes in community genetics [23]. Genes interact with the habitat and construct the phenotypes of the organisms, so they have foreseeable impacts on community phenotypes. The gene by habitat interactions could control the co-heritabilities of population phenotypes and as well as regulate the co-heritabilities of community phenotypes too. Habitat includes not only the abiotic elements but also the habitat that is created by the intergenomic epistatic interactions among the species [24].

In community genetics, different items like IEQ effect (Φ), habitat or environment effect (ɛ), IEQ by habitat interactions (Φ by ɛ), IEQ by IEQ interactions or intergenomic epistatic QTL interaction effects (Φ by ɛ), and also the higher-order interactions ( by Φ by ɛ) are important effects in the study of eco-evolutionary processes. Thus, interspecific interactions turn the classic QTL by habitat interactions into IEQ by IEQ by habitat interactions (Φ by Φ by ɛ) version that is defined as interspecific epistasis [2]. In ecological and eco-evolutionary genetics, these kinds of interactions and their phenotypic plasticities are important to study. In the communities living in non-homogeneous habitats, since different genotypes are expressed in various habitats, the plasticity is considered adaptive plasticity [26,27].

In eco-evolution studies, it is necessary to use genetic variations in one species that trigger the genetic changes in another species, therefore the impacts of genotype-by-genotype interactions on multilevel fitness are the promoters of eco-evolutionary dynamics [28]. In the epistatic model, a phenotype is created by the interactions among two or many genes, i.e., epistasis is a genetic feature that determines the eco-evolutionary paths and helps to transmit eco-evolutionary cycles between generations. Therefore, in biodiversity studies, the epistatic effects and genotype-by-genotype-by-environment interactions have high importance [28]. In physiological genetics and eco-evolutionary genetics, the interactions among two or many genes are defined as biochemical interactions and mathematical interactions, respectively [2].

According to the epistatic model, mutations that happen at various intergenomic sites could influence the multilevel fitness of species and their mean progeny number in the community through different biological pathways [30]. But, when genes of one species interact with particular genes in another organism, intergenomic epistasis takes place. Eco-evolution of IEQ is related to both environment and eco-evolutionary conditions of the community. In other words, when some species interact unsystematically with each other, the orientation and pressure of multilevel selection on a species rely on the average value of the environment produced by the other species [31]. As Keister et al. [32] have reported, this eco-evolution occurs in species, among the traits. Therefore, in community genetics (which unifies community ecology and genetics), the co-heritability of genes responds to natural multilevel selection. Some scientists believe that the most probable discipline to merge the biosciences arises in community genetics. The genes that create a phenotype in one organism can settle in the genome of another species and help to co-spread of them. Therefore, the result of natural multilevel selection on individuals of a specific species relies on genetic variability in a population of another species [2].

Intergenomic epistasis results from the interactions of genes from one species with particular genes in another species. For example, the epistasis among some plants and specific rhizobia is defined as intergenomic epistasis. These relationships cause trait correlations between species and lead to retaining the species interactions continuously. The presence of considerable intergenomic epistasis is a confirmation of interactive co-evolution, but hybridization tends to break co-adaptation through unifying nonnuclear and nuclear genomes [33]. In community genetics, genotype-by-genotype interaction (intergenomic epistasis) supports adaptive genetic co-variation through multilevel selection which is very dynamic in time and space, causing multilevel fitness [34].

In community genetics, recognizing the specific paths from genes to communities is crucial. In some studies, co-heritable genetic effects are satisfied with community genetics models and lead to introduce the extended phenotypes in foundation species which are the outcomes of gene actions at levels higher than the population level. Various individuals of the same species display extensive dissimilar indirect genetic effects. Hence, the extended phenotype could be regarded as the effects of genes at levels higher than the population level which is considered the indirect effect of genes [11].

In community genetics, the extended phenotypes of IEQ are inherited between the successive generations and, co-heritability of the extended phenotypes can be estimated but, the degree of co-heritability is varying [16]. The strong document for this co-heritability is the inheritance of the extended phenotypes among generations in community genetics. The genetic analysis of extended phenotypes can be achieved by a) Evolutionary genetics models, b) Population and quantitative genetics models, c) QTL mapping, d) Association mapping, e) Genome investigations, f) Gene expression surveys, and g) Candidate gene assessments. Also, it is important to study the genetic basis of the eco-evolutionary dynamics of IEQ by multivariate quantitative genetics analysis, genome scanning methods, and gene expression models [16]. Community genetics is not only prestigious knowledge but also is a wealthy interdisciplinary science, so it is worth studying and researching it. Thus, the aim of this paper was dynamical modeling of interspecific QTLs under slight and hard multilevel selections in an ecosystem to investigate eco-evolutionary genetic relationships among QTLs of multispecies.

Methods

Discrete-time modeling of IEQ dynamics for one species

It is possible to use the models of Mendelian and multivariate quantitative genetics to investigate eco-evolutionary community genetics since community phenotypes have a genomic basis that is co-heritable [24]. IEQ is a complicated interaction because it is consisting of many genes with small effects [35-37]. Therefore, in this paper, an unsystematically mating large diploid community including one species (number of species N =1) with separate generations is considered, and for simplicity, I show ith IEQ by Φ_i. Here, community refers to a population consisting of just one species, and IEQ refers to intergenomic epistatic QTL among the individuals of this community. Also, I define θ IEQ as Φ1,…, Φθ where $\theta \ge 1$ . The frequency of Φ_i in generation t is displayed by, $v_i=v_i\left(t\right)$ , where $v={\left(v_1,\mathrm{...},v_{\theta }\right)}^T$ is the vector of all Φ_i frequencies, and T denotes the matrix transposition.

In eco-evolutionary community genetics studies, fitness has a fundamental role and determines the phenotype’s capability to be survived and reproduced. In the discrete-time model, fitness is also expressed as Wrightian fitness. I show the multilevel fitness of the community by Ω. The multilevel fitness of an IEQ by IEQ interaction is explained through its phenotype-by-phenotype interaction which is influenced by the varying habitat. This multilevel fitness may be contrary to other habitats [38,39]. Therefore, multilevel fitness of Φ_i Φj (IEQ by IEQ interaction) is shown by ${\Omega }_{ij}={\Omega }_{ji}\rangle 0$ [40]. Multilevel fitness of IEQ, Ωi, and average multilevel fitness of community, $\stackrel{\_}{\Omega }$ , is defined as ${\Omega }_i={\Omega }_i(v)={\displaystyle \sum _j^{}{\Omega }_{ij}}{v}_j$ , and $\stackrel{\_}{\Omega }=\stackrel{-}{\Omega }(v)={\displaystyle \sum _i^{}{\Omega }_i}{v}_i={\displaystyle \sum _{i,j}^{}{\Omega }_{ij}}{v}_i{v}_j$ , respectively.

Continuous-time modeling of IEQ dynamics for one species

In community genetics, foundation species force multilevel selection on other community organisms and cause genetic differences to be recognizably distinguished among members of the communities. Therefore, remarkable co-heritability in the community phenotypes can be established. Since the interspecific interactions and their multilevel fitness outcomes are influenced by co-heritable traits of organisms, then species living in a community exhibit continuous eco-evolutionary variation [14].

To achieve a continuous-time model for IEQ dynamics, it is possible to reformulate time as $\text{t}=\lfloor \frac{\gamma }{\zeta }\rfloor$ , and multilevel fitness as ${\Omega }_{ij}=1+\zeta {\mu }_{ij}$ , where ${\mu }_{ij}$ is defined as the Malthusian multilevel fitness of Φ_iΦj. It is reminded that in a continuous-time model, fitness is also expressed as the Malthusian (simple exponential) fitness. Let ${\mu }_i={\displaystyle \sum _i^{}{\mu }_{ij}}{v}_j$ , and $\stackrel{}{\stackrel{-}{\mu }}={\displaystyle \sum _{i,j}^{}{\mu }_{ij}}{v}_i{v}_j$ denote the marginal multilevel fitness for IEQ and the mean of marginal multilevel fitness of community respectively; Also, let $u_i=u_i(\gamma )=v_i(t)$ , then as $\zeta \to 0$ , the limit of $\frac{\left[u_i\left(\gamma +\zeta \right)-u_i\left(\gamma \right)\right]}{\zeta }$ is computed. For more details, refer to Bürger (2011).

If the habitat term, ε, is defined as a Gaussian unsystematic variable with an average of zero, and no IEQ-by-habitat interactions exist, then the phenotypic value, π, for IEQ is specified as π = Φ + ε, in which the habitat and QTL terms, i.e. ε and Φ, are not correlated [40]. Let Φ be additive and equal to the total effects of QTL of a species at a particular genome. Therefore, the phenotypic covariance based on additive genetic covariance is explained as $Co{v}_{\pi }^{}=Co{v}_{\alpha }^{}+Co{v}_{\epsilon }^{}$ , where $Co{v}_{\pi }^{}$ is defined as total phenotypic covariance and $Co{v}_{\alpha }^{}$ is defined as additive genetic covariance. I show the average phenotypic effects before and after multilevel selection by ${\stackrel{\_}{\pi }}_{\text{b}}$ and ${\stackrel{\_}{\pi }}_{\text{a}}$ respectively.

Modeling of IEQ dynamics among N species

Some studies have shown that the interspecies interactions can regulate community reply to habitat fluctuations, as well as climate change. It has been clear that genomes of each species that live together in a particular environment perform the main role in community genetics, but it is not easy to understand how distinct species interact and make contact with each other. Despite the abundance of genetic data based on high-throughput genotyping and sequencing procedures, it is difficult to construct an accurate phenotype-genotype relation for interspecies interactions in community genetics [41].

Usually, the covariance matrices are considered fixed in theoretical modeling and data analysis, and most of the articles consider the related matrices as static. But, in complicated problems, the covariance matrices act dynamically in different conditions, especially in genetics, social sciences, and economic time series. Thus, in a high dimensional system like community genetics, because of the complexity and dimensionality, it is necessary to apply a kind of dynamic covariance analysis to study non-asymptotic biological rates and to model the multilevel selection features to distinguish varying correlations and covariance matrices [26]. Some evolutionary covariance software has been proposed to raise the accuracy of analyses [42,43]. The style of genetic co-variation for characters under multilevel selection is explained by Φ a matrix that specifies the magnitude and path of eco-evolutionary responses. Investigating the eco-evolution of correlated characters has high importance in eco-evolutionary genetics [44].

Thus, I suppose that ${\stackrel{\_}{\Psi }}_r$ to be the mean value of the IEQ state that is the expressed in rth species, where r = 1,…, N. Here, I define the IEQ state as the expression of an IEQ in a species. Therefore, if similar alleles contribute to IEQ states in species, then there are intergenomic correlations among species [45]. The additive genetic covariance of IEQ states in rth and sth species makes the elements of ${\Phi }_{rs}$ the matrix [46,47]. Also, ${\lambda }_r$ is defined as the proportion of the community in which rth species is migrated where ${\displaystyle \sum {\lambda }_r=1}$ , ${{\rm H}}_{rr}^{-1}$ is defined as the inverse of phenotypic covariance for rth species, and ${\varsigma }_r$ is defined as the difference between mean phenotype by phenotype, former and later of multilevel selection in rth species.

Software

In this paper MathType software, version 7.4.2.480 (1990-2019 WIRIS America, Design Science, Inc) was used to type the mathematical equations.

Results

Discrete-time dynamics of IEQ for one species

The frequency ( $v_i^{\prime }$ ) of Φ_i for one species in next-generation was determined as

$v_i^{\prime }=v_i\frac{{\Omega }_i}{\stackrel{-}{\Omega }}$ , for i = 1,…, θ , (1)

and the frequency of IEQ × IEQ interaction I, j was defined as $\frac{v_i{v}_j{\Omega }_{ij}}{\stackrel{\_}{\Omega }}$ . Following the reproduction, the frequency of Φ_i in the next generation was defined as $v_i^{\prime }={\displaystyle \sum _{j,l}^{}\frac{Z_{i,jl}{v}_j{v}_l{\Omega }_{jl}}{\stackrel{\_}{\Omega }}}$ , where $Z_{i,jl}$ was the probability to create Φ_i by random mating with ${\displaystyle \sum _i^{}{v}_i}=1$ .

Therefore, based on the simplex, ${\Im }_{\theta }=\left\{v={(v_1,\mathrm{...},v_{\theta })}^T\in {\Re }^{\theta }:{\displaystyle \sum _i^{}{v}_i=1,v_i\ge 0,i=1,\mathrm{...},\theta }\right\}$ , I considered a discrete-time dynamical system for one species. Recall that a simplex (or a hyper tetrahedron) is defined as the generalization of the idea of a triangle (or a tetrahedral region of space) to the higher dimensions [48]. Also, ${\prod }_0=\left\{v:v_i=v_{i_1}^{\left(1\right)}\cdot \mathrm{...}\cdot v_{i_L}^{\left(L\right)}\right\}\subseteq {\Im }_{\theta }$ indicates Wright’s manifold, such that $Y_i=0$ for each $v\in {\prod }_0$ . Therefore,

${\prod }_0\subseteq \left\{v:Y\text{}=0\right\},\text{ (2)}$

Where $Y={\left(Y_1,\mathrm{...},Y_{\theta }\right)}^T$ was defined as the vector of total linkage disequilibria. Therefore the equality was detained in submanifold (2) if multilevel selection did not occur. For more details, refer to Bürger [35]. It is reminded that if a topological space is locally Euclidean, then it is defined as a manifold. Wright’s manifold has a basic contribution to dynamical analysis in population genetics and community genetics under different sorts of selection forces.

Continuous-time dynamics of IEQ for one species

By replacing $v_i$ and t, instead of $u_i$ and $\gamma$ I acquired weak multilevel selection estimation as

$\stackrel{·}{v_i}=\frac{d{v}_i}{dt}=v_i\left({\mu }_i-\stackrel{\_}{\mu }\right),i=1,\mathrm{...},\theta .\text{ (3)}$

Thus, I had a continuous-time dynamical system on the simplex ${\Im }_{\theta }$ for one species having the same stabilities. To study additional details, refer to Bürger (2011). Also, let

${\Gamma }_i\left({\Phi }_m{\Phi }_n\right)=\{\begin{array}{l}1\text{if}m=n=i,\\ 0.5\text{if}m\ne n\text{and}m=i\text{or}n=i.\\ 0\text{otherwise,}\end{array}\text{ (4)}$

In system )4(, I was considered fixed but, m and n had the probability distribution Ƒ, and were not correlated. Therefore, the frequency of IEQ for a genotype-by-genotype interaction with expectation ${\text{v}}_i$ was estimated ${\Gamma }_i$ . Let $\Phi {}_v=\left({\phi }^{ij}\right)$ , which was a $\theta \times \theta$ genetic covariance (IEQ covariance) matrix for one species, where

${\phi }^{ij}=Cov\left({\Gamma }_i,{\Gamma }_j\right)=\frac{1}{2}{v}_i\left({\delta }_{ij}-v_j\right).\text{ (5)}$

In matrix (5) ${\delta }_{ij}$ , was Kronecker’s delta and defined as ${\delta }_{ij}=\{\begin{array}{l}0\text{}\text{if}i\ne j\\ 1\text{}\text{}\text{if}i=j\end{array}$ . Hence, continuous-time dynamical system )3( for one species was determined as a generalized gradient system on the simplex ${\Im }_{\theta }$

$\stackrel{·}{v}=\Phi {}_v\nabla \stackrel{\_}{\mu }=\Phi {}_v{\left(\frac{\partial \stackrel{\_}{\mu }}{\partial v_1},\mathrm{...},\frac{\partial \stackrel{\_}{\mu }}{\partial v_n}\right)}^T\text{ (6)}$

See Svirezhev [49] and Shahshahani [50].

It is reminded that in mathematics the simplest synonym for the gradient explains as slope, but in vector analysis, the gradient defines as a vector derivative operator $\nabla$ named Del and is applied to real functions of variables. Also, the direction $\nabla$ is determined as the orientation that the directional derivative shows the biggest value.

To perceive the dynamics of community genetics, determining the genetic covariance between two species is necessary [14]. Genetic covariance was partitioned into additive, dominance, and epistatic terms, thus the narrow-sense co-heritability, ${\hslash }^2{}_{narrow}$ , was calculated as the additive genetic covariance divided by the sum of phenotypic covariance: ${\hslash }^2{}_{narrow}=\frac{Co{v}_{\alpha }^{}}{Co{v}_{\pi }^{}}$ .

Because the habitat was considered to be a Gaussian unsystematic variable with an average zero, $\stackrel{\_}{\pi }=\stackrel{\_}{\Phi }$ , therefore the multilevel selection response between generations was determined $\Delta \stackrel{\_}{\pi }={\hslash }^2{}_{narrow}\left(\stackrel{\_}{{\pi }_b}-\stackrel{\_}{{\pi }_a}\right)$ . According to Robertson [51,52] and Bürger [40], response to multilevel selection based on a univariate linear parent-offspring regression was

$\Delta \stackrel{\_}{\Phi }=\frac{Co{v}_{\alpha }\left(\Phi ,\Omega \right)}{\stackrel{\_}{\Omega }},\text{ (7)}$

Where, $\Omega =\Omega \left(\Phi \right)$ demonstrated the multilevel fitness of the species with QTL value Φ, and $Co{v}_{\alpha }\left(\Phi ,\Omega \right)$ was specified as the additive genetic covariance of Φ, and $\Omega$ . By supposing weak multilevel selection relative to minimum recombination rate, ${\vartheta }_{\min }$ , i.e., $\zeta \ll {\vartheta }_{\min }$ , Nagylaki [53] had proved an asymptotic version of Eq. 7 as $\Delta \stackrel{\_}{\Phi }=\frac{Co{v}_{\alpha }\left(\Phi ,\Omega \right)}{\stackrel{\_}{\Omega }}+\ell \left({\zeta }^2\right)$ . For more details, refer to Nagylaki [53].

Lande [54] explained a theory to investigate the eco-evolutionary dynamics of complex phenotypes. The independency of Φ and ε from each other, plus the multivariate normal distributions were Lande’s main assumptions. A vector of value estimations for up to θ IEQs demonstrated the phenotypic values for species, i.e., $\pi ={\left({\pi }_1,\mathrm{...},{\pi }_{\theta }\right)}^T$ was described by an additive genetic component Φ, and a habitat residual ε such that $\pi =\Phi +\epsilon$ , where ε had average zero, i.e. $\stackrel{\_}{\pi }=\stackrel{\_}{\Phi }$ $\phi +\hat{\phi }$ . Therefore, Φ -Matrix was equaled to, which $\phi$ was the vector of IEQ estimates and $\hat{\phi }$ was the vector of genomic context estimates) [55].

IEQ dynamics among N species

A dynamical system for slight multilevel selection for N species was determined as,

$\left(\begin{array}{l}\Delta \stackrel{}{{\stackrel{-}{\Psi }}_1}\\ \Delta \stackrel{}{{\stackrel{-}{\Psi }}_2}\\ \Delta \stackrel{}{{\stackrel{-}{\Psi }}_3}\\ ⋮\\ \Delta \stackrel{}{{\stackrel{-}{\Psi }}_N}\end{array}\right)=\left(\begin{array}{l}\begin{array}{ccc}\begin{array}{l}{\Phi }_{11}\\ {\Phi }_{21}\\ {\Phi }_{31}\end{array}& \begin{array}{l}\cdots \\ \cdots \end{array}& \begin{array}{l}{\Phi }_{1N}\\ {\Phi }_{2N}\\ {\Phi }_{3N}\end{array}\\ ⋮& \ddots & ⋮\\ {\Phi }_{N1}& \cdots & {\Phi }_{NN}\end{array}\\ \end{array}\right)\left(\begin{array}{cc}\begin{array}{l}{\lambda }_1{{\rm H}}_{11}^{-1}\\ {\lambda }_2{{\rm H}}_{22}^{-1}\\ {\lambda }_3{{\rm H}}_{33}^{-1}\\ ⋮\end{array}& \begin{array}{l}{\varsigma }_1\\ {\varsigma }_2\\ {\varsigma }_3\\ ⋮\end{array}\\ {\lambda }_N{{\rm H}}_{NN}^{-1}& {\varsigma }_N\end{array}\right).$

The systems for three and two species were respectively as follows:

$\left(\begin{array}{l}\Delta \stackrel{}{{\stackrel{-}{\Psi }}_1}\\ \Delta \stackrel{}{{\stackrel{-}{\Psi }}_2}\\ \Delta \stackrel{}{{\stackrel{-}{\Psi }}_3}\end{array}\right)=\left(\begin{array}{ccc}{\Phi }_{11}& {\Phi }_{12}& {\Phi }_{13}\\ {\Phi }_{21}& {\Phi }_{22}& {\Phi }_{23}\\ {\Phi }_{31}& {\Phi }_{32}& {\Phi }_{33}\end{array}\right)\left(\begin{array}{cc}{\lambda }_1{{\rm H}}_{11}^{-1}& {\varsigma }_1\\ \begin{array}{l}{\lambda }_2{{\rm H}}_{22}^{-1}\\ {\lambda }_3{{\rm H}}_{33}^{-1}\end{array}& \begin{array}{l}{\varsigma }_2\\ {\varsigma }_3\end{array}\end{array}\right),$

$\left(\begin{array}{l}\Delta \stackrel{}{{\stackrel{-}{\Psi }}_1}\\ \Delta \stackrel{}{{\stackrel{-}{\Psi }}_2}\end{array}\right)=\left(\begin{array}{cc}{\Phi }_{11}& {\Phi }_{12}\\ {\Phi }_{21}& {\Phi }_{22}\end{array}\right)\left(\begin{array}{cc}{\lambda }_1{{\rm H}}_{11}^{-1}& {\varsigma }_1\\ {\lambda }_2{{\rm H}}_{22}^{-1}& {\varsigma }_2\end{array}\right).\text{ (8)}$

Therefore,

$\begin{array}{l}\text{Δ}\stackrel{}{{\stackrel{\text{-}}{\text{Ψ}}}_{\text{1}}}=\lambda {\Phi }_{11}{{\rm H}}_{11}^{-1}{\varsigma }_1+\left(1-\lambda \right){\Phi }_{12}{{\rm H}}_{22}^{-1}{\varsigma }_2\\ \text{Δ}\stackrel{}{{\stackrel{\text{-}}{\text{Ψ}}}_{\text{2}}}=\lambda {\Phi }_{21}{{\rm H}}_{11}^{-1}{\varsigma }_1+\left(1-\lambda \right){\Phi }_{22}{{\rm H}}_{22}^{-1}{\varsigma }_2\end{array}\}\text{ (9)}$

where $\lambda =\lambda {}_1=\lambda {}_2$ [45]. Eq. 9 demonstrates that if IEQ was expressed in related species, then the eco-evolution of IEQ states promoted the response to multilevel selection. Therefore, when two IEQ states were co-selected, i.e., ${\varsigma }_1>0\text{ , and }{\varsigma }_2>0\text{, }\lambda =0.5$ , a small genetic covariance in species, i.e., ${\Phi }_{12}$ diminished the size of co-evolution. On the other hand, eco-evolution in interruptive multilevel selection i.e. ${\varsigma }_1>0\text{ and }{\varsigma }_2<0$ was detained through positive genetic covariance. When IEQ was promoted in each species, the multilevel selection on other IEQ was proceeded, resulting in varying the mean phenotype.

The multilevel fitness of the phenotype $\Psi$ in rth species was demonstrated as ${\Omega }_r\left({\Psi }_r\right)$ . The phenotypes, $v_r\left({\Psi }_r\right)$ and had normal distribution and the mean multilevel fitness was shown by $\stackrel{}{{\stackrel{-}{\Omega }}_r}$ , therefore, the multilevel selection differential in rth species was defined as [45].

${\varsigma }_r=\frac{\left[{\displaystyle \int {\Psi }_r{v}_r\left({\Psi }_r\right){\Omega }_r\left({\Psi }_r\right)d{\Psi }_r}\right]}{\stackrel{}{{\stackrel{-}{\Omega }}_r}-\stackrel{}{{\stackrel{-}{\Psi }}_r}}\text{ (10)}$

According to the Eq. 10 and variations in mean multilevel fitness accompanied by a growing change $\stackrel{}{{\stackrel{-}{\Psi }}_r}$ , the expected multilevel selection differential was reformulated based on the gradient of mean multilevel fitness in rth species as follows

${{\rm H}}_{rr}^{-1}{\zeta }_r={\nabla }_r\ln \stackrel{}{{\stackrel{-}{\Omega }}_r},\text{ (11)}$

where the gradient derivative operator ${\nabla }_r=\frac{\partial }{\partial {\stackrel{-}{\Psi }}_r}$ acting on $\ln \stackrel{}{{\stackrel{-}{\Omega }}_r}$ explained the outcome of multilevel selection in rth species on IEQ state (Lande 1979). The partial regression coefficient of the relative multilevel fitness in rth species $\frac{{\Omega }_r}{{\stackrel{-}{\Omega }}_r}$ on ${\Psi }_r$ was identical to the multilevel selective pressure ${\nabla }_r\ln \stackrel{}{{\stackrel{-}{\Omega }}_r}$ [56]. Substituting Eq. 11 into Eq. 8 showed the dynamical system for slight multilevel selection for two species that were reformulated as

$\left(\begin{array}{l}\Delta \stackrel{}{{\stackrel{-}{\Psi }}_1}\\ \Delta \stackrel{}{{\stackrel{-}{\Psi }}_2}\end{array}\right)=\left(\begin{array}{cc}{\Phi }_{11}& {\Phi }_{12}\\ {\Phi }_{21}& {\Phi }_{22}\end{array}\right).\left(\begin{array}{l}{\nabla }_1\\ {\nabla }_2\end{array}\right)\ln \left[\stackrel{}{\stackrel{-}{\Omega }{}_1^{\lambda }}\stackrel{}{\stackrel{-}{\Omega }{}_2^{\left(1-\lambda \right)}}\right].\text{ (12)}$

The geometric average of the mean multilevel fitness for two species explained Wright’s idea of an adaptive topography for eco-evolution of two species, where the topography was defined as a diagram of average community multilevel fitness versus the gene frequencies. Therefore, the equation $\stackrel{}{\stackrel{-}{\Omega }}=\stackrel{}{\stackrel{-}{\Omega }{}_1^{\lambda }}\stackrel{}{\stackrel{-}{\Omega }{}_2^{1-\lambda }}$ specified the joint mean multilevel fitness under the slight multilevel selection [45].

Eco-evolutionary dynamics of mean multilevel fitness were evaluated by expanding around a selected point. If a slight multilevel selection took place, then the higher-order terms were omitted. Hence, I had $\Delta \ln \left[\stackrel{-}{\Omega }{}_1^{\lambda }\stackrel{-}{\Omega }{}_2^{\left(1-\lambda \right)}\right]=\left(\Delta \stackrel{}{{\stackrel{-}{\Psi }}_1},\Delta \stackrel{}{{\stackrel{-}{\Psi }}_2}\right).\nabla \ln \left[\stackrel{-}{\Omega }{}_1^{\lambda }\stackrel{-}{\Omega }{}_2^{\left(1-\lambda \right)}\right]={\left(\nabla \ln \stackrel{-}{\Omega }\right)}^T\Phi \nabla \ln \stackrel{-}{\Omega }\ge 0$ , where ${\nabla }^T=\left({\nabla }_1,{\nabla }_2\right)$ .

A dynamical system for phenotypic eco-evolution under hard multilevel selection for two species was demonstrated as,

$\left(\begin{array}{l}\Delta \stackrel{}{{\stackrel{-}{\Psi }}_1}\\ \Delta \stackrel{}{{\stackrel{-}{\Psi }}_2}\end{array}\right)=\left(\begin{array}{cc}{\Phi }_{11}& {\Phi }_{12}\\ {\Phi }_{21}& {\Phi }_{22}\end{array}\right).\left(\begin{array}{l}{\nabla }_1\\ {\nabla }_2\end{array}\right)\ln \left[\lambda \stackrel{}{{\stackrel{-}{\Omega }}_1}+\left(1-\lambda \right)\stackrel{}{{\stackrel{-}{\Omega }}_2}\right]\text{ (13)}$

where, $\stackrel{}{\stackrel{-}{\Omega }}=\lambda \stackrel{}{{\stackrel{-}{\Omega }}_1}+\left(1-\lambda \right)\stackrel{}{{\stackrel{-}{\Omega }}_2}$ , and the relative mean multilevel fitness of selected species was $\frac{\stackrel{}{{\stackrel{-}{\Omega }}_r}}{\stackrel{-}{\Omega }}$ . Since $\frac{\partial \stackrel{}{{\stackrel{-}{\Omega }}_2}}{\partial {\stackrel{-}{\Psi }}_1}=0$ , so $\stackrel{}{{\stackrel{-}{\Omega }}_2}$ did not play the role as a function of $\stackrel{}{{\stackrel{-}{\Psi }}_1}$ , thus $\left(\lambda \frac{\stackrel{}{{\stackrel{-}{\Omega }}_1}}{\stackrel{-}{\Omega }}\right){\nabla }_1\ln \stackrel{}{{\stackrel{-}{\Omega }}_1}=\left(\frac{\lambda }{\stackrel{-}{\Omega }}\right)\left(\frac{\partial \stackrel{}{{\stackrel{-}{\Omega }}_1}}{\partial {\stackrel{-}{\Psi }}_1}\right)=\left(\frac{1}{\stackrel{-}{\Omega }}\right)\left[\frac{\lambda \partial \stackrel{}{{\stackrel{-}{\Omega }}_1}}{\partial {\stackrel{-}{\Psi }}_1}+\frac{\left(1-\lambda \right)\partial \stackrel{}{{\stackrel{-}{\Omega }}_2}}{\partial {\stackrel{-}{\Psi }}_1}\right]={\nabla }_1\ln \stackrel{-}{\Omega }$ [45].

The multilevel fitness of species demonstrating phenotype π was defined as, $\Omega (\pi )$ , and $g\left(\pi \right)$ showed Gaussian density of phenotypes. Thus, the average multilevel fitness of a community was explained as

$\stackrel{-}{\Omega }={\displaystyle \int g\left(\pi \right)}\Omega \left(\pi \right)d\pi \text{ (14)}$

which was a function of $\stackrel{\_}{\pi }$ and π.

The change of average phenotype between generations was proved by Lande [46,47,54] as follows:

$\Delta \stackrel{\_}{\pi }=\Phi \nabla ln\stackrel{-}{\Omega }=\Phi {\left(\frac{\partial \ln \stackrel{-}{\Omega }}{\partial \stackrel{\_}{{\pi }_1}},\mathrm{...},\frac{\partial \ln \stackrel{-}{\Omega }}{\partial \stackrel{\_}{{\pi }_{\theta }}}\right)}^T,\text{ (15)}$

where $\nabla \ln \stackrel{-}{\Omega }$ was defined as the multilevel selection gradient, and was equated to Robertson’s Eq. 7 in the univariate model? Here, the analogy with Shahshahani’s [50] - Svirezhev’s [[49] gradient in Eq. 6 was noticeable. Also, Eq. 15 specified $\Delta \ln \stackrel{-}{\Omega }\ge 0$ . Therefore, IEQ analysis was integrated into community genetics based on Lande’s assumptions. The dominance and epistatic effects were incorporated into the multilevel fitness since the multilevel fitness function was nonlinear [40].

Discussion

Discrete-time and Continuous-time dynamics of IEQ for one species

Maintaining the interactions among species possessing genetic origin is an essential feature for conservation programs in community genetics [15]. Various defending strategies, and life cycle plans, the eco-evolution of phenotypic plasticity, male and female multilevel fitness, and the eco-evolution of drought resistance are examples of eco-evolutionary ecological responses [44].

Due to the multilevel fitness of the community and genotype-by-genotype interactions, I considered Robertson’s equation for the response to multilevel selection (Eq. 7(. Therefore, I formulated the discrete-time dynamical system for eco-evolution of intergenomic epistatic QTL (IEQ) frequencies in one species (Eq. 1(. According to Eq. 6, it was shown that the continuous-time dynamical system for eco-evolution of IEQ frequencies in one species was determined as a generalized gradient $\nabla$ system on the simplex ${\Im }_{\theta }$ .

According to Price’s equation [57] and based on the population parameters, the fundamental theorem of evolution can be partitioned into the fundamental theorem of gene selection and the fundamental theorem of phenotypic selection (Robertson’s equation 1966, 1968). Price [57,58]declared that the covariance between fitness and trait could explain the variation in a quantitative trait [6].

Fisher (1930) [59] in his fundamental theorem of natural selection declared that the mean fitness was increased by natural selection at a degree identical to the additive genetic variance for fitness [60]. The primary thesis of Fisher was that genetic variation and natural selection work together in a fundamental way ensuring fitness increase in natural populations which was a mathematical proof of Darwinian evolution.

Eco-evolutionary dynamics of IEQ among N species

To merge eco-evolutionary genetic and ecosystem dynamics, a community genetic diversity model based on a dynamic system was considered [61]. In community genetics, community disequilibria which were defined as the remaining co-heritability among interrelating species played important roles in meta-populations studies and response to multilevel selection [3].

In the present work, Eq. 9 demonstrated that if intergenomic epistatic QTL (IEQ) was expressed in related species, then eco-evolution of IEQ states promoted the response to multilevel selection, and eco-evolution in interruptive multilevel selection was maintained through positive genetic covariance. Anyway, when IEQ was promoted in each species, the multilevel selection on other IEQ was proceeded to vary the phenotype mean. In population-level investigations that were based on pedigree relations and multivariate selection, multivariate quantitative genetics was applied to analyze the evolutionary reactions [62].

Pedruzzi [29] reported that both biochemical interactions including epigenetic effects and different gene actions were responsible to express the variability of inherited characters. Therefore, turning eco-evolutionary biology to the cell-to-cell signal transferring in eukaryotic organisms, along with cellular differentiation as epigenetic changes, has uncovered the biology to its basis such that the complete organism is considered as a mapping from genome to phenome. Also, fractal geometry was often used to study the co-adaptation of organisms with the habitat [63].

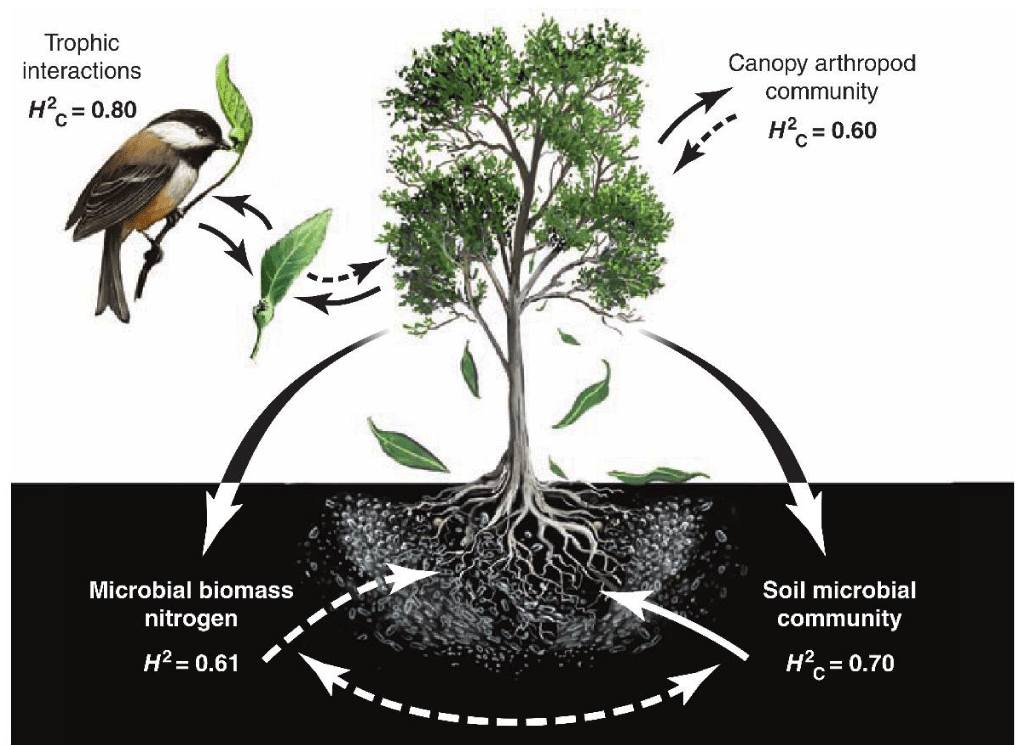
Figure 3 shows an example of epigenetic processes in community genetics that affect the characters in foundation species and community co-heritability.

Figure 3: The genotypes of Populus Angustifolia presented broad-sense co-heritability in their community genetics. This community included the trees of Populus Angustifolia, soil microbes, trophic relations among insects and birds, arthropods, plus soil nutrients. Here, H² showed the heritability of one community character while H²_C showing the co-heritability of community characters. Continuous arrows designated the usual interrelations and dotted arrows specified the probable interrelations. Figure reproduced with permission from REF. Whitham, © [14] Science, www.sciencemag.org.

These quantitative motifs demonstrated that co-heritability of particular community phenotypes determined a genomics achievement that joined co-changing genetic interrelations. The trees of Populus Angustifolia revealed nearly sixty percent of co-heritability in the arthropods community. These analyses connected community characters with foundation species and genome sequences, since they verified genetic support for community phenotypes [14].

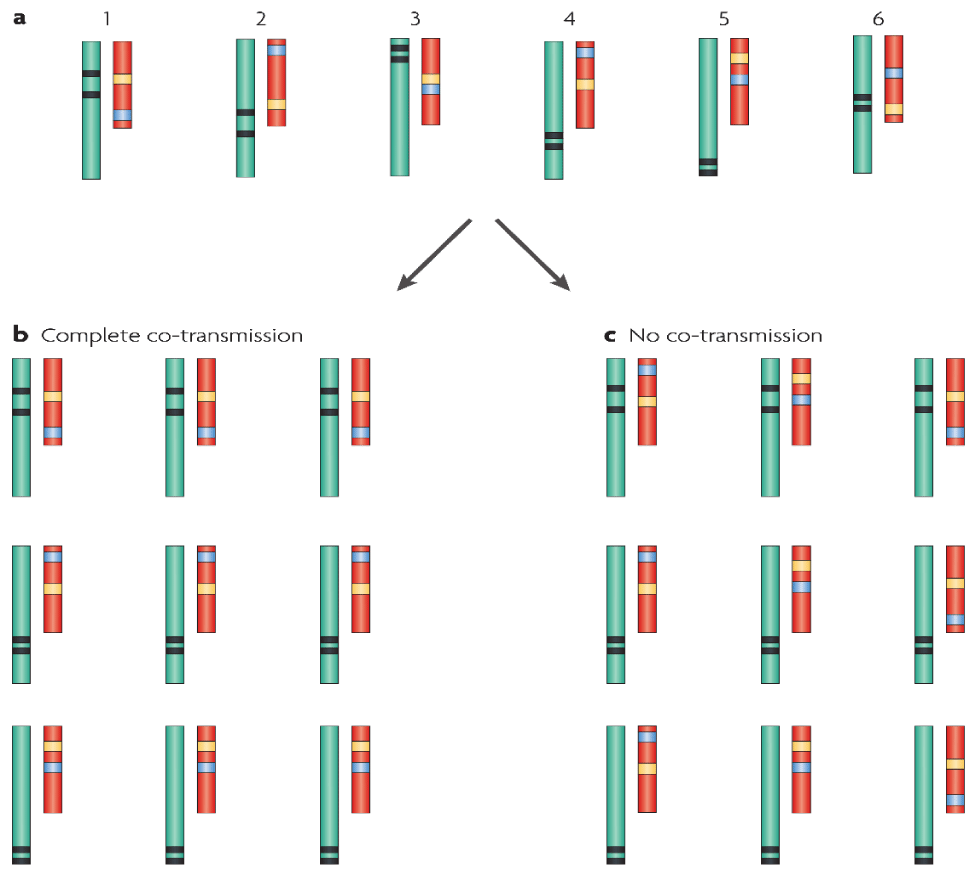
The co-heritability of gene compositions is presented in Figure 4, where each host and its related parasite have been genotyped through different molecular markers.

Figure 4: The schematic co-heritability of genes. The amount of co-heritability was determined with a set of host species, such as the six hosts in part a or the nine hosts in parts b, and c. In this figure, the host genes were shown in green with different markers in black, and parasite genes were shown in red with different markers in blue and yellow. The host-parasite set in part a showed the parents of the offspring host-parasite set in parts b and c. Specific parasite genotypes were congregated as stated by the host genotype with a sizable co-heritability, as in part b. But in the absence of co-heritability, as in part c, there was no observable relationship between the genotypes of parasite and host. Figure reproduced with permission from REF. Wade, © [2] Nature publishing group.

The vertical inheritance of a parasite from parent to offspring was the same as the maternal co-heritability of mitochondria that was taken place in lots of plants and animals. In the areas of decreased recombination, e.g., in the mitochondria, the genes were co-heritable with features that were the same as those of unlinked genes. In unsystematically huge mating populations, where the linkage of the genes was trivial, there was small co-heritability. Therefore, the adaptive multilevel selection took place, if the multilevel selection on genes was severe. The genes that regulated co-transmission and correlated with the intergenomic epistatic compositions, could increase the rate of co-heritability [2].

Lamarck [64] declared that the capacity of habitat in eco-evolution could be considered epigenetic co-heritability. In other words, the cell-to-cell signal transferring established epigenetic co-heritability and shaped the links between the organism and its habitat for co-evolution. Therefore, connecting the epigenetic co-heritability and phenotypic effects was promoted to obtain the epigenetic traces [65].

In the present study, the expected multilevel selection differential was reformulated based on the gradient of the mean multilevel fitness in rth species as, ${{\rm H}}_{rr}^{-1}{\zeta }_r={\nabla }_r\ln \stackrel{}{{\stackrel{-}{\Omega }}_r}$ , in which the gradient operator ${\nabla }_r=\frac{\partial }{\partial {\stackrel{-}{\Psi }}_r}$ acting on $\ln \stackrel{}{{\stackrel{-}{\Omega }}_r}$ explained the outcome of multilevel selection in the rth species on the IEQ state.

I displayed that the dynamical system for slight multilevel selection for two species was demonstrated in Eq. 12 in which the weighted geometric average of the mean multilevel fitness presented an adaptive topography for co-evolution, and $\stackrel{}{\stackrel{-}{\Omega }}=\stackrel{}{\stackrel{-}{\Omega }{}_1^{\lambda }}\stackrel{}{\stackrel{-}{\Omega }{}_2^{1-\lambda }}$ determined the joint mean multilevel fitness. Based on eco-evolutionary genetic architecture responses, phenotypic plasticity caused trait changes among heterogeneous habitats [66,67].

A phenotype has been defined as the sum of the genetic and habitat effects on traits. But community phenotypes have emerged from co-relations with other species that coexisted in the community. For community phenotypes, the variations were correlated with foundation species and had a genetic basis that originated from indirect genetic effects (IGE), namely the phenotype of an individual was a portion of the habitat of another one. But, when the habitat effects on the phenotype of one species were because of the gene function in another organism, the interspecific indirect genetic effects (IIGE) took place [24]. When IIGE took place, eco-evolutionary genetic interactions among species in different individuals occurred, i.e., the indirect relations took place in community genetics (e.g., in plants and insect communities). Community phenotypes appeared due to both co-heritable characters in foundation species and the effects of these characters through IIGE on the multilevel fitness of other species. Therefore, the broad-sense community co-heritability was estimated in the area that the variations in community phenotypes were controlled by genetic changes within foundation species [24].

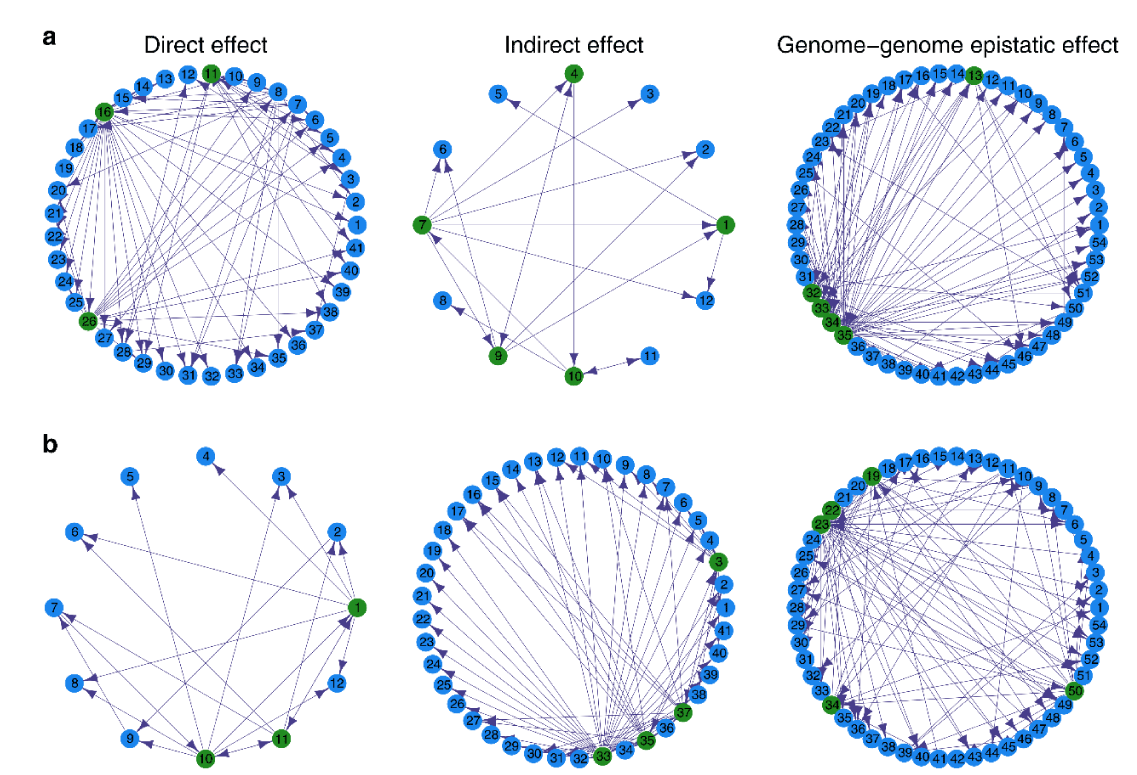
Figure 5 is an example of the development of Escherichia coli and related QTL networks that are regulated through direct effects of its 41 single nucleotide polymorphisms, and indirect effects of 12 single nucleotide polymorphisms belonging to Staphylococcus aureus and interspecific epistatic effects among the single nucleotide polymorphisms.

Figure 5: Various kinds of genetic effects and related QTL networks. Panel a: Forty-one QTL with direct effects in Escherichia coli, twelve QTL with indirect effects in Staphylococcus aureus, and also, QTL with intergenomic epistatic effects associated with the development of Escherichia coli. Panel b: Twelve QTL with direct effects in Staphylococcus aureus, forty-one QTL with indirect effects in Escherichia coli, and also, QTL with intergenomic epistatic effects associated with the development of Staphylococcus aureus. Triggering a QTL by another QTL path was shown by the straight thin arrows. Further information about these QTLs was presented in Jiang (2018). Figure reproduced with permission from REF. Jiang, © [41] Nature Communications.

Twelve S. aureus QTL and 41 E. coliM QTL turned on the indirect and direct effects of the growth of S. aureus respectively. Here, the QTL network was studied based on an ordinary differential equation model to determine how QTL interactions had worked. The development of E. coliM and S. aureus in a complicated changeable network were intervened through genome-by-genome epistatic effects [41].

In the present work, the dynamic system for phenotypic eco-evolution under hard multilevel selection for two species (Eq. 13(, and the relative mean multilevel fitness of selected species was estimated as $\frac{\stackrel{}{{\stackrel{-}{\Omega }}_r}}{\stackrel{-}{\Omega }}$ . Achievements in community genetics were justified if huge genotypic changes in characters showed a basic contribution to intergenomic epistatic interactions [68].

Besides, the mean multilevel fitness of the community was demonstrated through Eq. 14 and the change of average phenotype between generations was explained through Eq. 15 which $\nabla \ln \stackrel{-}{\Omega }$ demonstrated the multilevel selection gradient. The dominance and epistatic effects were incorporated into the multilevel fitness since the multilevel fitness function was nonlinear. Therefore, IEQ analysis was integrated into the community genetics. The mathematical models have revealed that when genes were linked to the X chromosomes, the intergenomic interactions could be assisted in retaining the polymorphism [69].

Another important subject is epigenome. An epigenome includes a set of chemical changes to the DNA and histone proteins of an entity (plant, animal, etc.). These changes can be handed down to an organism’s offspring via transgenerational stranded epigenetic inheritance. Changes to the epigenome can result in changes to the structure of chromatin and changes to the function of the genome. The epigenome is involved in tissue differentiation, development, regulating gene expression, and suppression of transposable elements. Unlike the genome which remains mostly unchanged within an individual, the epigenome can be dynamically changed by habitat conditions [70].

Moreover, the epigenome comprising different mechanisms e.g., DNA methylation, remodeling, histone tail modifications, chromatin microRNAs, and long non-coding RNAs, interact with environmental factors like nutrition, pathogens, and climate to influence the expression profile of genes and the emergence of specific phenotypes [71-74]. Multi-level interactions between the genome, epigenome, and environmental factors might occur [75]. Furthermore, numerous lines of evidence suggest the influence of epigenome variation on health and production [72,76].

Future achievement

I propose to consider a) communities with small size and random genetic drift, b) mathematical modeling of non-random mating communities, c) asexual reproduction, and d) complete epigenetic effects to analyze the eco-evolutionary dynamics of intergenomic epistatic QTL under slight and hard multilevel selections in future studies of community genetics. For such studies, multiallelic loci and polygenic inheritance need to be assessed because of the connections between homozygosity and the frequency of genes at polymorphic loci [77]. Since the multilevel fitness of the genotype-by-genotype interactions are not exactly fixed parameters and are usually correlated to other different variables, it is important to investigate them accompanied by abiotic and biotic stress conditions in heterogeneous environments.

Perspectives of higher-level research

Since exact relationships between specific genes and ecosystems are not clear yet, it is crucial to mathematically analyze the new problems in community genetics, accompanied by genetic marker technologies, DNA-RNA sequencing, and comparative genomics. Therefore, the perspective of this paper is mathematical modeling and analysis of the rich and attractive problems in eco-evolutionary molecular IEQ to construct an approximately accurate phenotype-genotype relationship in community genetics and co-speciation networks. Co-speciation is a kind of co-evolution in which the speciation of one species dictates the speciation of another species. This is necessary to achieve the goal, i.e., to get closer to unifying biosciences. Therefore, I think that a challenging interdisciplinary science will probably arise from this perspective.

Final suggestion

Finally, I propose that mathematicians, statisticians, community geneticists, and ecologists combine the mathematical and theoretical modeling with experimental designs and practical laboratory, and field studies including natural populations of organisms to increase the accuracy and precision of predictions between empirical and theoretical investigations.

I have to thank Prof. Andrew P. Hendry, Redpath Museum, Department of Biology, McGill University, Canada; Prof. Thomas G. Whitham, Department of Biological Sciences, Northern Arizona University, USA; Prof. Michael J. Wade, Department of Biology, Indiana University, USA and Prof. Rongling Wu, Pennsylvania State University, Department of Public Health Sciences, the USA for permitting me to reuse Figures 2-5, respectively. I also have to appreciate Prof. Joseph Felsenstein Professor Emeritus of Genome Science and Biology, Department of Genome Sciences, University of Washington, Seattle, and Dr. Lynn Govaert, Group leader at Leibniz-Institute of freshwater ecology and inland fisheries (IGB), Berlin, Germany for their valuable comments.

1. Miko I. Gregor Mendel and the principles of inheritance. Nat Edu. 2008; 1: 134.
2. Wade MJ. The co-evolutionary genetics of ecological communities. Nat Rev Genet. 2007 Mar;8(3):185-95. doi: 10.1038/nrg2031. Epub 2007 Feb 6. PMID: 17279094.
3. Whitham TG, Young WP, Martinsen GD, Gehring CA, Schweitzer JA, Shuster S. Community and ecosystem genetics: A consequences of the extended phenotype. Ecology, 2003; 84: 559-573.
4. Lander ES, Schork NJ. Genetic dissection of complex traits. Science. 1994 Sep 30;265(5181):2037-48. doi: 10.1126/science.8091226. Erratum in: Science 1994 Oct 21;266(5184):353. PMID: 8091226.
5. Morin PJ. Community ecology and the genetics of interacting species. Ecology. 2003; 84: 577-580.
6. Ellner SP, Geber MA, Hairston NG Jr. Does rapid evolution matter? Measuring the rate of contemporary evolution and its impacts on ecological dynamics. Ecol Lett. 2011 Jun;14(6):603-14. doi: 10.1111/j.1461-0248.2011.01616.x. Epub 2011 Apr 24. PMID: 21518209.
7. Dobzhansky T. Genetics and the Origin of Species. 3rd ed. Columbia University Press, New York.  1951.
8. Ford EB. Ecological Genetics and Evolution. Blackwell Scientific Publication.  1971.
9. Ricklefs RE. Genetics, evolution, and ecological communities. Ecology. 2003; 84, 588-591.  
10. Antonovics J. Toward community genomics? Ecology. 2003; 84, 598-601. 
11. Wilson DS, Swenson W. Community genetics and community selection. Ecology. 2003; 84, 586-588.
12. Neuhauser C, Andow DA, Heimpel GE, May G, Shaw RG, Wagenius S. Community genetics: expanding the synthesis of ecology and genetics. Ecology. 2003; 84, 545-558.
13. Crutsinger GM. A community genetics perspective: opportunities for the coming decade. New Phytol. 2016 Apr;210(1):65-70. doi: 10.1111/nph.13537. Epub 2015 Jul 14. PMID: 26171846.
14. Whitham TG, DiFazio SP, Schweitzer JA, Shuster SM, Allan GJ, Bailey JK. Extending genomics to natural communities and ecosystems. Science. 2008; 320: 492-495.
15. Collins JP. What can we learn from community genetics? Ecology. 2003; 84: 574-577.
16. Hendry AP. Key questions in the genetics and genomics of eco-evolutionary dynamics. Heredity (Edinb). 2013 Dec;111(6):456-66. doi: 10.1038/hdy.2013.75. Epub 2013 Aug 21. PMID: 23963343; PMCID: PMC3833688.
17. Govaert, L, Fronhofer EA, Lion S, Eizaguirre C, Bonte D, Egas M. Eco-evolutionary feedbacks-Theoretical models and perspectives. Funct. Ecol. 2018; 1-18.
18. Govaert L, Pantel JH, De Meester L. Eco-evolutionary partitioning metrics: assessing the importance of ecological and evolutionary contributions to population and community change. Ecol Lett. 2016 Aug;19(8):839-53. doi: 10.1111/ele.12632. Epub 2016 Jun 24. PMID: 27339378.
19. Cavender-Bares J, Wilczek A. Integrating micro-and macroevolutionary processes in community ecology. Ecology. 2003; 84: 592-597.
20. Mackay TF, Stone EA, Ayroles JF. The genetics of quantitative traits: challenges and prospects. Nat Rev Genet. 2009 Aug;10(8):565-77. doi: 10.1038/nrg2612. PMID: 19584810.
21. Wu R, Lin M. Functional mapping - how to map and study the genetic architecture of dynamic complex traits. Nat Rev Genet. 2006 Mar;7(3):229-37. doi: 10.1038/nrg1804. PMID: 16485021.
22. DeWoody J, Viger M, Lakatos F, Tuba K, Taylor G, Smulders MJ. Insight into the genetic components of community genetics: QTL mapping of insect association in a fast-growing forest tree. PLoS One. 2013 Nov 19;8(11):e79925. doi: 10.1371/journal.pone.0079925. PMID: 24260320; PMCID: PMC3833894.
23. Mitchell-Olds T, Willis JH, Goldstein DB. Which evolutionary processes influence natural genetic variation for phenotypic traits? Nat Rev Genet. 2007 Nov;8(11):845-56. doi: 10.1038/nrg2207. PMID: 17943192.
24. Whitham TG, Bailey JK, Schweitzer JA, Shuster SM, Bangert RK, LeRoy CJ, Lonsdorf EV, Allan GJ, DiFazio SP, Potts BM, Fischer DG, Gehring CA, Lindroth RL, Marks JC, Hart SC, Wimp GM, Wooley SC. A framework for community and ecosystem genetics: from genes to ecosystems. Nat Rev Genet. 2006 Jul;7(7):510-23. doi: 10.1038/nrg1877. PMID: 16778835.
25. Ungerer MC, Halldorsdottir SS, Purugganan MD, Mackay TF. Genotype-environment interactions at quantitative trait loci affecting inflorescence development in Arabidopsis thaliana. Genetics. 2003 Sep;165(1):353-65. doi: 10.1093/genetics/165.1.353. PMID: 14504242; PMCID: PMC1462760.
26. Chen Z, Leng C. Dynamic covariance models. J Amer Stat Ass 2016; 111: 1196-1207.
27. Chen X, Zhao F, Xu S. Mapping environment-specific quantitative trait loci. Genetics. 2010 Nov;186(3):1053-66. doi: 10.1534/genetics.110.120311. Epub 2010 Aug 30. PMID: 20805558; PMCID: PMC2975292.
28. TerHorst CP, Zee PC, Heath KD, Miller TE, Pastore AI. Evolution in a community context: Trait responses to multiple species interactions. Am Nat. 2018; 191(3).
29. Pedruzzi G, Barlukova A, Rouzine IM. Evolutionary footprint of epistasis. PLoS Comput Biol. 2018 Sep 17;14(9):e1006426. doi: 10.1371/journal.pcbi.1006426. PMID: 30222748; PMCID: PMC6177197.
30. Pedruzzi G, Rouzine IM. Epistasis detectably alters correlations between genomic sites in a narrow parameter window. PLoS One. 2019 May 31;14(5):e0214036. doi: 10.1371/journal.pone.0214036. PMID: 31150393; PMCID: PMC6544209.
31. Wade M.J. Community genetics and species interactions. Ecology. 2003; 84, 583-585.
32. Keister AR, Lande R, Schemske DW. Models of coevolution and speciation in plants and their pollinators. Am Nat. 1984; 124: 220-243.
33. Wade MJ, Drown DM. Nuclear–mitochondrial epistasis: a gene’s eye view of genomic conflict. Ecol Evol. 2016; 6: 6460-6472.
34. Heath KD. Intergenomic epistasis and coevolutionary constraint in plants and rhizobia. Evolution. 2010 May;64(5):1446-58. doi: 10.1111/j.1558-5646.2009.00913.x. Epub 2009 Nov 26. PMID: 20002161.
35. Bürger R. The Mathematical Theory of Selection, Recombination, and Mutation. Wiley, Chichester. 2000.
36. Mackay TF. The genetic architecture of quantitative traits. Annu Rev Genet. 2001;35:303-39. doi: 10.1146/annurev.genet.35.102401.090633. PMID: 11700286.
37. Barton NH, Keightley PD. Understanding quantitative genetic variation. Nat Rev Genet. 2002 Jan;3(1):11-21. doi: 10.1038/nrg700. PMID: 11823787.
38. Ewens WJ. Mathematical Population Genetics. 2nd edition. Springer, New York. 2003.
39. James FC, Kimura M. An Introduction to Population Genetics Theory. Blackburn Press, New Jersey. 1970.
40. Bürger R. Some Mathematical Models in Evolutionary Genetics. Springer, Berlin. 2011.
41. Jiang L, He X, Jin Y, Ye M, Sang M, Chen N, Zhu J, Zhang Z, Li J, Wu R. A mapping framework of competition-cooperation QTLs that drive community dynamics. Nat Commun. 2018 Aug 1;9(1):3010. doi: 10.1038/s41467-018-05416-w. PMID: 30068948; PMCID: PMC6070507.
42. Simkovic F, Thomas JM, Keegan RM, Winn MD, Mayans O, Rigden DJ. Residue contacts predicted by evolutionary covariance extend the application of ab initio molecular replacement to larger and more challenging protein folds. IUCrJ. 2016 Jun 15;3(Pt 4):259-70. doi: 10.1107/S2052252516008113. PMID: 27437113; PMCID: PMC4937781.
43. Lakhani B, Thayer KM, Hingorani MM, Beveridge DL. Evolutionary covariance combined with molecular dynamics predicts a framework for allostery in the MutS DNA mismatch repair protein. J Phys Chem B 121: 2049-2061.
44. Simonsen AK, Stinchcombe JR. Quantifying evolutionary genetic constraints in the Ivyleaf Morning Glory, Ipomoea hederacea. Int J Plant Sci 2010; 171: 972-986.
45. Via S. Lande R. Genotype-environment interaction and the evolution of phenotypic plasticity. Evolutio. 1985; 39, 505-522.
46. Lande R. The maintenance of genetic variability by mutation in a polygenic character with linked loci. Genet Res. 1975 Dec;26(3):221-35. doi: 10.1017/s0016672300016037. PMID: 1225762.
47. Lande R. The genetic covariance between characters maintained by pleiotropic mutations. Genetics. 1980; 94: 203-215.
48. Buekenhout F, Parker M. The number of nets of the regular convex polytopes in dimensions ≤ 4. Disc Math. 1998; 186: 69-94.
49. Svirezhev, Yu M. Optimality principles in population genetics. In: Studies in theoretical genetics, Institute of Cytology and Genetics, Novosibirsk, 1972; 86-102. (In Russian)
50. Shahshahani S. A new mathematical framework for the study of linkage and selection. Mem. Am. Math. Soc. 1979; 17: ix+34.
51. Robertson A. A mathematical model of the culling process in dairy cattle. Anim Prod 1966; 8: 95-108.
52. Robertson A. The spectrum of genetic variation. In: Lewontin RC (ed) Population biology and evolution, University Press, Syracuse. 1968; 5-16.
53. Nagylaki T. The evolution of multilocus systems under weak selection. Genetics. 1993 Jun;134(2):627-47. doi: 10.1093/genetics/134.2.627. PMID: 8325492; PMCID: PMC1205503.
54. Lande R. QUANTITATIVE GENETIC ANALYSIS OF MULTIVARIATE EVOLUTION, APPLIED TO BRAIN:BODY SIZE ALLOMETRY. Evolution. 1979 Mar;33(1Part2):402-416. doi: 10.1111/j.1558-5646.1979.tb04694.x. PMID: 28568194.
55. Kelly JK. Connecting QTLS to the g-matrix of evolutionary quantitative genetics. Evolution. 2009 Apr;63(4):813-25. doi: 10.1111/j.1558-5646.2008.00590.x. Epub 2008 Dec 12. PMID: 19087179; PMCID: PMC5972393.
56. Lande R, Arnold SJ. THE MEASUREMENT OF SELECTION ON CORRELATED CHARACTERS. Evolution. 1983 Nov;37(6):1210-1226. doi: 10.1111/j.1558-5646.1983.tb00236.x. PMID: 28556011.
57. Price GR. Selection and covariance. Nature. 1970 Aug 1;227(5257):520-1. doi: 10.1038/227520a0. Erratum in: Nature. 1970 Dec 5;228(5275):1011. PMID: 5428476.
58. Price GR. Extension of covariance selection mathematics. Ann Hum Genet. 1972 Apr;35(4):485-90. doi: 10.1111/j.1469-1809.1957.tb01874.x. PMID: 5073694.
59. Fisher RA. The Genetical Theory of Natural Selection. Oxford University Press, Oxford. 1930.
60. Queller DC. Fundamental Theorems of Evolution. Am Nat. 2017 Apr;189(4):345-353. doi: 10.1086/690937. Epub 2017 Feb 28. PMID: 28350496.
61. Overcast I, Emerson BC, Hickerson MJ. An integrated model of population genetics and community ecology. J. Biogeography. 2019; 46(4).
62. Melo D, Marroig G, Wolf  JB. Genomic perspective on multivariate variation, pleiotropy, and evolution. J Heredity. 2019; 1-15.
63. Torday JS. The Singularity of nature. Prog Biophys Mol Biol. 2019 Mar;142:23-31. doi: 10.1016/j.pbiomolbio.2018.07.013. Epub 2018 Aug 1. PMID: 30076851.
64. Lamarck JB. Philosophie Zoologique ou Exposition des Considérations Relatives à l'Histoire Naturelle des Animaux. Musée d'Histoire Naturelle (Jardin des Plantes). 1809.
65. Torday JS. Evolution, the ‘mechanism’ of big history-the grande synthesis. J Big Hist 2019; III: 17-24.
66. Allen B, McAvoy A. A mathematical formalism for natural selection with arbitrary spatial and genetic structure. J Math Biol. 2019; 78: 1147.
67. Leimar O, Dall SRX, McNamara JM, Kuijper B, Hammerstein P. Ecological Genetic Conflict: Genetic Architecture Can Shift the Balance between Local Adaptation and Plasticity. Am Nat. 2019 Jan;193(1):70-80. doi: 10.1086/700719. Epub 2018 Nov 21. PMID: 30624104.
68. Chase JM, Knight TF. Community genetics: Toward a synthesis. Ecology. 2003; 84, 580-582.
69. Dowling DK, Friberg U, Hailer F, Arnqvist G. Intergenomic epistasis for fitness: within-population interactions between cytoplasmic and nuclear genes in Drosophila melanogaster. Genetics. 2007 Jan;175(1):235-44. doi: 10.1534/genetics.105.052050. Epub 2006 Dec 6. PMID: 17151264; PMCID: PMC1774999.
70. Bernstein BE, Meissner A, Lander ES. The mammalian epigenome. Cell. 2007 Feb 23;128(4):669-81. doi: 10.1016/j.cell.2007.01.033. PMID: 17320505.
71. Barazandeh A, Mohammadabadi MR, Ghaderi-Zefrehei M, Rafeied F, Imumorin IG. Whole genome comparative analysis of CpG islands in camelid and other mammalian genomes. Mamm. Biol. 2019; 98: 73-79. 
72. Masoudzadeh SH, Mohammadabadi MR, Khezri A, Kochuk-Yashchenko OA, Kucher DM, Babenko OI. et al. Dlk1 gene expression in different Tissues of lamb. Iran. J. Appl. Anim. Sci. 2020; 10: 669-677.
73. Shahsavari M, Mohammadabadi M, Khezri A, Asadi Fozi M, Babenko O, Kalashnyk O, Oleshko V, Tkachenko S. Correlation between insulin-like growth factor 1 gene expression and fennel (Foeniculum vulgare) seed powder consumption in muscle of sheep. Anim Biotechnol. 2021 Nov 16:1-11. doi: 10.1080/10495398.2021.2000997. Epub ahead of print. PMID: 34783639.
74. Mohamadipoor L, Mohammadabadi M, Amiri Z, Babenko O, Stavetska R, Kalashnik O, Kucher D, Kochuk-Yashchenko O, Asadollahpour H. Signature selection analysis reveals candidate genes associated with production traits in Iranian sheep breeds. BMC Vet. Res. 2021; 17(1): 1-9.
75. Mohammadabadi MR, Jafari AHD, Bordbar F. Molecular analysis of CIB4 gene and protein in Kermani sheep. Braz J Med Biol Res. 2017 Sep 12;50(11):e6177. doi: 10.1590/1414-431X20176177. PMID: 28902924; PMCID: PMC5597282.
76. Masoudzadeh SH, Mohammadabadi M, Khezri A, Stavetska RV, Oleshko VP, Babenko OI, Yemets Z, Kalashnik OM.  Effects of diets with different levels of fennel (Foeniculum vulgare) seed powder on DLK1 gene expression in brain, adipose tissue, femur muscle and rumen of Kermani lambs. Small Rumin Rese . 2020; 193: e106276.
77. Aw AJ, Rosenberg NA. Bounding measures of genetic similarity and diversity using majorization. J Math Biol. 2018 Sep;77(3):711-737. doi: 10.1007/s00285-018-1226-x. Epub 2018 Mar 22. PMID: 29569105; PMCID: PMC6133051.